MOLCAS manual:

Subsections

• 6.3.1 GATEWAY Output
• 6.3.2 Basis Set Superposition Error (BSSE)
• 6.3.3 GATEWAY Basic and Most Common Keywords

6.3 GATEWAY - Definition of geometry, basis sets, and symmetry

The program GATEWAY handles the basic molecular parameters in the calculation. It generates data that are used in all subsequent calculations. These data are stored in the RUNFILE. GATEWAY is the first program to be executed, if the $WorkDir directory and the RUNFILE file has not already been generated by a previous calculation.

This tutorial is describes how to set up the basic MOLCAS input for the water molecule. For a more general description of the input options for GATEWAY, please refer to the Users Guide. The first line of the input is the program identifier &GATEWAY. Then follows the keyword used is TITLe which will also get printed in the GATEWAY section of the calculation output. The title line is also saved in the integral file and will appear in subsequent programs.

The GROUp keyword is followed by the generators for the C_2v point group, since the example deals with the water molecule. The specification of the C_2v point group given in Table 6.1 is not unique, but, in this tutorial, the generators have been input in an order that reproduces the ordering in the character tables. A complete list of symmetry generator input syntax is given in Table 6.1. The symmetry groups available are listed with the symmetry generators defining the group. The MOLCAS keywords required to specify the symmetry groups are also listed. The last column contains the symmetry elements generated by the symmetry generators.

  &GATEWAY
Title=  Water  in  C2v  symmetry  -  A  Tutorial
Coord  =  water.xyz
Group  =  XY  Y
Basis  Set  =  O.ANO-S-MB,H.ANO-S-MB

Table 6.1: Symmetries available in MOLCAS including generators, MOLCAS keywords and symmetry elements.

Group

Generators

MOLCAS

Elements

g1

g2

g3

g1

g2

g3

E

g1

g2

g1g2

g3

g1g3

g2g3

g1g2g3

C1

E

C2

C2

xy

E

C2

Cs

$\sigma$

x

E

$\sigma$

Ci

i

xyz

E

i

C2v

C2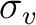

$\sigma_v$

xy

y

E

C2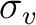

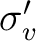$\sigma_v$

$\sigma_v'$

C2h

C2

i

xy

xyz

E

C2

i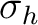

$\sigma_h$

D2

C2z

C2y

xy

xz

E

C2z

C2y

C2x

D2h

C2z

C2y

i

xy

xz

xyz

E

C2z

C2y

C2x

i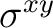

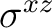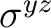$\sigma^{xy}$

$\sigma^{xz}$

$\sigma^{yz}$

To reduce the input, the unity operator E is always assumed. The twofold rotation about the z-axis, C₂(z), and the reflection in the xz-plane, 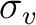$\sigma_v$(xz), are input as XY and Y respectively. The MOLCAS input can be viewed as symmetry operators that operate on the Cartesian elements specified. For example, the reflection in the xz-plane is specified by the input keyword Y which is the Cartesian element operated upon by the reflection.

The input produces the character table in the GATEWAY section of the output shown in Figure 6.3. Note that 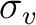$\sigma_v$(yz) was produced from the other two generators. The last column contains the basis functions of each irreducible symmetry representation. The totally symmetric a₁ irreducible representation has the z basis function listed which is unchanged by any of the symmetry operations.

                             E   C2(z) s(xz) s(yz)
                    a1       1     1     1     1  z
                    b1       1    -1     1    -1  x, xz, Ry
                    a2       1     1    -1    -1  xy, Rz, I
                    b2       1    -1    -1     1  y, yz, Rx

The geometry of the molecule is defined using the keyword coord. On the next line, the name of the xyz file that defines the geometrical parameters of the molecule (water.xyz) is given.

1. The first line of the water.xyz file contains the number of atoms.
2. The second line is used to indicate the units: Ångström or atomic units.

   The default is to use Ångström.

3. Then follows one line for each atom containing the name of each atom and its coordinates.

Basis sets are defined after the keyword BASIs sets. The oxygen and hydrogen basis set chosen, for this example, are the small Atomic Natural Orbitals (ANO) sets. There are three contractions of the basis included in the input, which can be toggled in or excluded with an asterisk, according to the desired calculation: minimal basis, double zeta basis with polarization, or triple zeta basis with polarization.

Figure 6.2: The geometry of the water molecule

 3

O	       .000000        .000000	     .000000  
H	      0.700000        .000000	    0.700000 
H	     -0.700000        .000000	    0.700000

6.3.1 GATEWAY Output

The GATEWAY output contains the symmetry character table, basis set information and input atomic centers. The basis set information lists the exponents and contraction coefficients as well as the type of Gaussian functions (Cartesian, spherical or contaminated) used.

The internuclear distances and valence bond angles (including dihedral angles) are displayed after the basis set information. Inertia and rigid-rotor analysis is also included in the output along with the timing information.

A section of the output that is useful for determining the input to the MOLCAS module SCF is the symmetry adapted basis functions which appears near the end of the GATEWAY portion of the output. This is covered in more detail in the SCF tutorial.

The most important file produced by the GATEWAY module is the RUNFILE which in our case is linked to water.RunFile. This is the general MOLCAS communications file for transferring data between the various MOLCAS program modules. Many of the program modules add data to the RUNFILE which can be used in still other modules. A new RUNFILE is produced every time GATEWAY is run. It should finally be mentioned that for backwards compatibility one can run MOLCAS without invoking GATEWAY. The corresponding input and output will then be handled by the program SEWARD.

6.3.2 Basis Set Superposition Error (BSSE)

GATEWAY can operates with several coordinate files, which is convenient for computing BSSE corrections. BSSE followed by a number marks a XYZ file which should be treated as dummy atoms. The following example demonstrates this feature:

&GATEWAY
coord  =  ethanol.xyz
coord  =  water.xyz
bsse  =  1
basis  =  ANO-S-MB
NOMOVE
&SEWARD;  &SCF
&GRID_IT
NAME  =  water
***************
&GATEWAY
coord  =  ethanol.xyz
coord  =  water.xyz
bsse  =  2
basis  =  ANO-S-MB
NOMOVE
&SEWARD;  &SCF
&GRID_IT
NAME  =  ethanol
**************
&GATEWAY
coord  =  ethanol.xyz
coord  =  water.xyz
basis  =  ANO-S-MB
NOMOVE
&SEWARD;  &SCF
&GRID_IT
NAME  =  akvavit

Note, that NOMOVE keyword prevents centering of the molecule, so the computed grids are identical. An alternative way to compute density difference is to modify coordinates, and change an element label to X.

6.3.3 GATEWAY Basic and Most Common Keywords

Keyword	Meaning
Coord	File name or inline number of atoms and XYZ coordinates
BASIs Set	Atom_label.Basis_label (for example ANO-L-VTZP)
Group	Full (find maximum), NoSym, or symmetry generators
SYMMetry	Symmetry generators: X, Y, Z, XY, XZ, YZ, XYZ (in native format)
RICD	On-the-fly auxiliary basis sets.