





















MOLCAS manual: Next: 10.2 Geometry optimizations and Hessians. Up: 10. Examples Previous: 10. Examples
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Symmetry | Spherical harmonics | |||||
 |
s | pz | dz2 | fz3 | ||
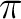 |
px | py | dxz | dyz | fx(z2-y2) | fy(z2-x2) |
 |
dx2-y2 | dxy | fxyz | fz(x2-y2) | ||
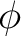 |
fx3 | fy3 | ||||
In C2v, however, the functions are distributed into the four representations
of the group and therefore different symmetry representations can be mixed.
The next table lists the distribution of the
functions in C2v and the symmetry of the corresponding orbitals in 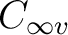 .
.
| Symm.a | Spherical harmonics (orbitals in 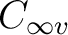 ) ) |
|||||
| a1 (1) | s ( ) ) |
pz ( ) ) |
dz2 ( ) ) |
dx2-y2 ( ) ) |
fz3 ( ) ) |
fz(x2-y2) ( ) ) |
| b1 (2) | px (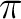 ) ) |
dxz (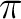 ) ) |
fx(z2-y2) (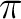 ) ) |
fx3 (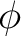 ) ) |
||
| b2 (3) | py (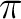 ) ) |
dyz (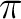 ) ) |
fy(z2-x2) (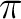 ) ) |
fy3 (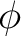 ) ) |
||
| a2 (4) | dxy ( ) ) |
fxyz ( ) ) |
||||
| aIn parenthesis the number of the symmetry in MOLCAS. It depends on the generators used in SEWARD. | ||||||
In symmetry 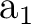 we find both
we find both  and
and  orbitals. When the
calculation is performed in C2v symmetry all the orbitals of
orbitals. When the
calculation is performed in C2v symmetry all the orbitals of 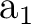 symmetry
can mix because they belong to the same representation, but this is not
correct for
symmetry
can mix because they belong to the same representation, but this is not
correct for 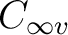 . The total symmetry must be kept
. The total symmetry must be kept 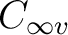 and therefore the
and therefore the
 orbitals should not be allowed to rotate and mix with the
orbitals should not be allowed to rotate and mix with the  orbitals. The same is true in the
orbitals. The same is true in the 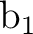 and
and 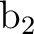 symmetries with the
symmetries with the 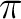 and
and
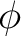 orbitals, while in
orbitals, while in 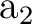 symmetry this problem does not exist because
it has only
symmetry this problem does not exist because
it has only  orbitals (with a basis set up to f functions).
orbitals (with a basis set up to f functions).
The tool to restrict possible orbital rotations is the option SUPSym in the RASSCF program. It is important to start with clean orbitals belonging to the actual symmetry, that is, without unwanted mixing.
But the problems with the symmetry are not solved with the SUPSym option only.
Orbitals belonging to different components of a degenerate representation should also be
equivalent. For example: the 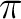 orbitals in
orbitals in 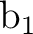 and
and 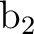 symmetries should have the
same shape, and the same is true for the
symmetries should have the
same shape, and the same is true for the  orbitals in
orbitals in 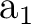 and
and 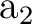 symmetries.
This can only be partly achieved in the RASSCF code. The input option AVERage
will average the density matrices for representations
symmetries.
This can only be partly achieved in the RASSCF code. The input option AVERage
will average the density matrices for representations 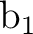 and
and 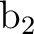 (
(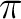 and
and 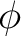 orbitals), thus producing equivalent orbitals. The present version does not, however,
average the
orbitals), thus producing equivalent orbitals. The present version does not, however,
average the  orbital densities in representations
orbital densities in representations 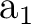 and
and 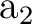 (note that
this problem does not occur for electronic states with an equal occupation of the
two components of a degenerate set, for example
(note that
this problem does not occur for electronic states with an equal occupation of the
two components of a degenerate set, for example 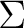 states).
A safe way to obtain totally symmetric orbitals is to reduce the symmetry to C1
(or Cs in the homonuclear case) and perform a state-average calculation for the
degenerate components.
states).
A safe way to obtain totally symmetric orbitals is to reduce the symmetry to C1
(or Cs in the homonuclear case) and perform a state-average calculation for the
degenerate components.
We need an equivalence table to know the correspondence of the symbols for the functions in MOLCAS to the spherical harmonics (SH):
| MOLCAS | SH | MOLCAS | SH | MOLCAS | SH | ||
| 1s | s | 3d2+ | dx2-y2 | 4f3+ | fx3 | ||
| 2px | px | 3d1+ | dxz | 4f2+ | fz(x2-y2) | ||
| 2pz | pz | 3d0 | dz2 | 4f1+ | fx(z2-y2) | ||
| 2py | py | 3d1- | dyz | 4f0 | fz3 | ||
| 3d2- | dxy | 4f1- | fy(z2-x2) | ||||
| 4f2- | fxyz | ||||||
| 4f3- | fy3 |
We begin by performing a SCF calculation and analyzing the resulting orbitals. The employed bond distance is close to the experimental equilibrium bond length for the ground state [241]. Observe in the following SEWARD input that the symmetry generators, planes yz and xz, lead to a C2v representation. In the SCF input we have used the option OCCNumbers which allows specification of occupation numbers other than 0 or 2. It is still the closed shell SCF energy functional which is optimized, so the obtained SCF energy has no physical meaning. However, the computed orbitals are somewhat better for open shell cases as NiH. The energy of the virtual orbitals is set to zero due to the use of the IVO option. The order of the orbitals may change in different computers and versions of the code.
&SEWARD
Title
NiH G.S
Symmetry
X Y
Basis set
Ni.ANO-L...5s4p3d1f.
Ni 0.00000 0.00000 0.000000 Bohr
End of basis
Basis set
H.ANO-L...3s2p.
H 0.000000 0.000000 2.747000 Bohr
End of basis
End of Input
&SCF
TITLE
NiH G.S.
OCCUPIED
8 3 3 1
OCCNumber
2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0
2.0 2.0 2.0
2.0 2.0 2.0
1.0
SCF orbitals + arbitrary occupations
~
Molecular orbitals for symmetry species 1
~
ORBITAL 4 5 6 7 8 9 10
ENERGY -4.7208 -3.1159 -.5513 -.4963 -.3305 .0000 .0000
OCC. NO. 2.0000 2.0000 2.0000 2.0000 2.0000 .0000 .0000
~
1 NI 1s0 .0000 .0001 .0000 -.0009 .0019 .0112 .0000
2 NI 1s0 .0002 .0006 .0000 -.0062 .0142 .0787 .0000
3 NI 1s0 1.0005 -.0062 .0000 -.0326 .0758 .3565 .0000
4 NI 1s0 .0053 .0098 .0000 .0531 -.4826 .7796 .0000
5 NI 1s0 -.0043 -.0032 .0000 .0063 -.0102 -.0774 .0000
6 NI 2pz .0001 .0003 .0000 -.0015 .0029 .0113 .0000
7 NI 2pz -.0091 -.9974 .0000 -.0304 .0622 .1772 .0000
8 NI 2pz .0006 .0013 .0000 .0658 -.1219 .6544 .0000
9 NI 2pz .0016 .0060 .0000 .0077 -.0127 -.0646 .0000
10 NI 3d0 -.0034 .0089 .0000 .8730 .4270 .0838 .0000
11 NI 3d0 .0020 .0015 .0000 .0068 .0029 .8763 .0000
12 NI 3d0 .0002 .0003 .0000 -.0118 -.0029 -.7112 .0000
13 NI 3d2+ .0000 .0000 -.9986 .0000 .0000 .0000 .0175
14 NI 3d2+ .0000 .0000 .0482 .0000 .0000 .0000 .6872
15 NI 3d2+ .0000 .0000 .0215 .0000 .0000 .0000 -.7262
16 NI 4f0 .0002 .0050 .0000 -.0009 -.0061 .0988 .0000
17 NI 4f2+ .0000 .0000 .0047 .0000 .0000 .0000 -.0033
18 H 1s0 -.0012 -.0166 .0000 .3084 -.5437 -.9659 .0000
19 H 1s0 -.0008 -.0010 .0000 -.0284 -.0452 -.4191 .0000
20 H 1s0 .0014 .0007 .0000 .0057 .0208 .1416 .0000
21 H 2pz .0001 .0050 .0000 -.0140 .0007 .5432 .0000
22 H 2pz .0008 -.0006 .0000 .0060 -.0093 .2232 .0000
~
ORBITAL 11 12 13 14 15 16 18
ENERGY .0000 .0000 .0000 .0000 .0000 .0000 .0000
OCC. NO. .0000 .0000 .0000 .0000 .0000 .0000 .0000
~
1 NI 1s0 -.0117 -.0118 .0000 .0025 .0218 -.0294 .0000
2 NI 1s0 -.0826 -.0839 .0000 .0178 .1557 -.2087 .0000
3 NI 1s0 -.3696 -.3949 .0000 .0852 .7386 -.9544 .0000
4 NI 1s0 -1.3543 -1.1537 .0000 .3672 2.3913 -2.8883 .0000
5 NI 1s0 -.3125 .0849 .0000 -1.0844 .3670 -.0378 .0000
6 NI 2pz -.0097 -.0149 .0000 .0064 .0261 -.0296 .0000
7 NI 2pz -.1561 -.2525 .0000 .1176 .4515 -.4807 .0000
8 NI 2pz -.3655 -1.0681 .0000 .0096 1.7262 -2.9773 .0000
9 NI 2pz -1.1434 -.0140 .0000 -.1206 .2437 -.9573 .0000
10 NI 3d0 -.1209 -.2591 .0000 .2015 .5359 -.4113 .0000
11 NI 3d0 -.3992 -.3952 .0000 .1001 .3984 -.9939 .0000
12 NI 3d0 -.1546 -.1587 .0000 -.1676 -.2422 -.4852 .0000
13 NI 3d2+ .0000 .0000 -.0048 .0000 .0000 .0000 -.0498
14 NI 3d2+ .0000 .0000 -.0017 .0000 .0000 .0000 -.7248
15 NI 3d2+ .0000 .0000 .0028 .0000 .0000 .0000 -.6871
16 NI 4f0 -.1778 -1.0717 .0000 -.0233 .0928 -.0488 .0000
17 NI 4f2+ .0000 .0000 -1.0000 .0000 .0000 .0000 -.0005
18 H 1s0 1.2967 1.5873 .0000 -.3780 -2.7359 3.8753 .0000
19 H 1s0 1.0032 .4861 .0000 .3969 -.9097 1.8227 .0000
20 H 1s0 -.2224 -.2621 .0000 .1872 .0884 -.7173 .0000
21 H 2pz -.1164 -.4850 .0000 .3388 1.1689 -.4519 .0000
22 H 2pz -.1668 -.0359 .0000 .0047 .0925 -.3628 .0000
~
Molecular orbitals for symmetry species 2
~
ORBITAL 2 3 4 5 6 7
ENERGY -3.1244 -.5032 .0000 .0000 .0000 .0000
OCC. NO. 2.0000 2.0000 .0000 .0000 .0000 .0000
~
1 NI 2px -.0001 .0001 .0015 .0018 .0012 -.0004
2 NI 2px -.9999 .0056 .0213 .0349 .0235 -.0054
3 NI 2px -.0062 -.0140 .1244 -.3887 .2021 -.0182
4 NI 2px .0042 .0037 .0893 .8855 -.0520 .0356
5 NI 3d1+ .0053 .9993 .0268 .0329 .0586 .0005
6 NI 3d1+ -.0002 -.0211 -.5975 .1616 .1313 .0044
7 NI 3d1+ -.0012 -.0159 .7930 .0733 .0616 .0023
8 NI 4f1+ .0013 -.0049 .0117 .1257 1.0211 -.0085
9 NI 4f3+ -.0064 .0000 -.0003 -.0394 .0132 .9991
10 H 2px -.0008 .0024 -.0974 -.1614 -.2576 -.0029
11 H 2px .0003 -.0057 -.2060 -.2268 -.0768 -.0079
~
Molecular orbitals for symmetry species 3
~
ORBITAL 2 3 4 5 6 7
ENERGY -3.1244 -.5032 .0000 .0000 .0000 .0000
OCC. NO. 2.0000 2.0000 .0000 .0000 .0000 .0000
~
1 NI 2py -.0001 .0001 -.0015 .0018 .0012 .0004
2 NI 2py -.9999 .0056 -.0213 .0349 .0235 .0054
3 NI 2py -.0062 -.0140 -.1244 -.3887 .2021 .0182
4 NI 2py .0042 .0037 -.0893 .8855 -.0520 -.0356
5 NI 3d1- .0053 .9993 -.0268 .0329 .0586 -.0005
6 NI 3d1- -.0002 -.0211 .5975 .1616 .1313 -.0044
7 NI 3d1- -.0012 -.0159 -.7930 .0733 .0616 -.0023
8 NI 4f3- .0064 .0000 -.0003 .0394 -.0132 .9991
9 NI 4f1- .0013 -.0049 -.0117 .1257 1.0211 .0085
10 H 2py -.0008 .0024 .0974 -.1614 -.2576 .0029
11 H 2py .0003 -.0057 .2060 -.2268 -.0768 .0079
~
Molecular orbitals for symmetry species 4
~
ORBITAL 1 2 3 4
ENERGY -.0799 .0000 .0000 .0000
OCC. NO. 1.0000 .0000 .0000 .0000
~
1 NI 3d2- -.9877 -.0969 .0050 -.1226
2 NI 3d2- -.1527 .7651 .0019 .6255
3 NI 3d2- -.0332 -.6365 -.0043 .7705
4 NI 4f2- .0051 -.0037 1.0000 .0028
In difficult situations it can be useful to employ the AUFBau option of the SCF program. Including this option, the subsequent classification of the orbitals in the different symmetry representations can be avoided. The program will look for the lowest-energy solution and will provide with a final occupation. This option must be used with caution. It is only expected to work in clear closed-shell situations.
We have only printed the orbitals most relevant to the following discussion.
Starting with symmetry 1 (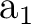 ) we observe that the orbitals
are not mixed at all. Using a basis set contracted to Ni 5s4p3d1f / H 3s2p
in symmetry
) we observe that the orbitals
are not mixed at all. Using a basis set contracted to Ni 5s4p3d1f / H 3s2p
in symmetry 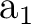 we obtain 18
we obtain 18  molecular orbitals (combinations
from eight atomic s functions,
six pz functions, three dz2 functions, and one fz3 function)
and four
molecular orbitals (combinations
from eight atomic s functions,
six pz functions, three dz2 functions, and one fz3 function)
and four  orbitals (from three dx2-y2 functions and one
fz(x2-y2) function). Orbitals 6, 10, 13, and 18 are formed by contributions from
the three dx2-y2 and one
fz(x2-y2)
orbitals (from three dx2-y2 functions and one
fz(x2-y2) function). Orbitals 6, 10, 13, and 18 are formed by contributions from
the three dx2-y2 and one
fz(x2-y2)  functions, while the
contributions of the remaining harmonics are zero. These orbitals are
functions, while the
contributions of the remaining harmonics are zero. These orbitals are  orbitals
and should not mix with the remaining
orbitals
and should not mix with the remaining 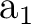 orbitals.
The same situation occurs in symmetries
orbitals.
The same situation occurs in symmetries 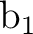 and
and 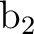 (2 and 3) but in this case
we observe an important mixing among the orbitals. Orbitals 7
(2 and 3) but in this case
we observe an important mixing among the orbitals. Orbitals 7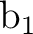 and 7
and 7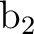 have main contributions from the harmonics 4f3+ (fx3) and 4f3- (fy3),
respectively. They should be pure
have main contributions from the harmonics 4f3+ (fx3) and 4f3- (fy3),
respectively. They should be pure
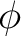 orbitals and not mix at all with the remaining
orbitals and not mix at all with the remaining 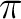 orbitals.
orbitals.
The first step is to evaluate the importance of the mixings
for future calculations. Strictly, any kind of mixing should be avoided.
If g functions are used, for instance, new contaminations show up. But,
undoubtedly, not all mixings are going to be equally important. If the
rotations occur among occupied or active orbitals the influence
on the results is going to be larger than if they are high secondary
orbitals. NiH is one of these cases. The ground state of the molecule
is 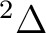 . It has two components and we can therefore compute it
by placing the single electron in the dxy orbital (leading to a
state of
. It has two components and we can therefore compute it
by placing the single electron in the dxy orbital (leading to a
state of 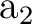 symmetry in C2v) or in the dx2-y2 orbital of the
symmetry in C2v) or in the dx2-y2 orbital of the
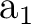 symmetry. Both are
symmetry. Both are  orbitals and the resulting states
will have the same energy provided that no mixing happens. In the
orbitals and the resulting states
will have the same energy provided that no mixing happens. In the
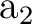 symmetry no mixing is possible because it is only composed
of
symmetry no mixing is possible because it is only composed
of  orbitals but in
orbitals but in 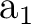 symmetry the
symmetry the  and
and  orbitals
can rotate. It is clear that this type of mixing will be more
important for the calculation than the mixing of
orbitals
can rotate. It is clear that this type of mixing will be more
important for the calculation than the mixing of 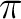 and
and 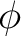 orbitals. However it might be necessary to prevent it. Because in the
SCF calculation no high symmetry restriction was imposed on the orbitals,
orbitals 2 and 4
of the
orbitals. However it might be necessary to prevent it. Because in the
SCF calculation no high symmetry restriction was imposed on the orbitals,
orbitals 2 and 4
of the 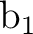 and
and 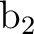 symmetries have erroneous contributions of
the 4f3+ and 4f3- harmonics, and they are occupied or active
orbitals in the following CASSCF calculation.
symmetries have erroneous contributions of
the 4f3+ and 4f3- harmonics, and they are occupied or active
orbitals in the following CASSCF calculation.
To use the supersymmetry (SUPSym) option we must
start with proper orbitals. In this case the 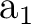 orbitals are
symmetry adapted (within the printed accuracy) but not the
orbitals are
symmetry adapted (within the printed accuracy) but not the
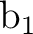 and
and 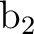 orbitals. Orbitals 7
orbitals. Orbitals 7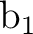 and 7
and 7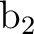 must have zero coefficients for all the harmonics except for
4f3+ and 4f3-, respectively. The remaining orbitals of these
symmetries (even those not shown) must have zero in the
coefficients corresponding to 4f3+ or 4f3-. To clean the orbitals
the option CLEAnup of the RASSCF program can be used.
must have zero coefficients for all the harmonics except for
4f3+ and 4f3-, respectively. The remaining orbitals of these
symmetries (even those not shown) must have zero in the
coefficients corresponding to 4f3+ or 4f3-. To clean the orbitals
the option CLEAnup of the RASSCF program can be used.
Once the orbitals are properly symmetrized we can perform CASSCF calculations on different electronic states. Deriving the types of the molecular electronic states resulting from the electron configurations is not simple in many cases. In general, for a given electronic configuration several electronic states of the molecule will result. Wigner and Witmer derived rules for determining what types of molecular states result from given states of the separated atoms. In chapter VI of reference [243] it is possible to find the tables of the resulting electronic states once the different couplings and the Pauli principle have been applied.
In the present CASSCF calculation we have chosen the active
space (3d, 4d,  ,
, 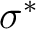 ) with all the 11 valence
electrons active. If we consider 4d and
) with all the 11 valence
electrons active. If we consider 4d and 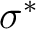 as weakly occupied
correlating orbitals, we are left with 3d and
as weakly occupied
correlating orbitals, we are left with 3d and  (six orbitals),
which are to be occupied with 11 electrons. Since the bonding
orbital
(six orbitals),
which are to be occupied with 11 electrons. Since the bonding
orbital  (composed mainly of Ni 4s and H 1s) will be doubly
occupied in all low lying electronic states, we are left with nine
electrons to occupy the 3d orbitals. There is thus one hole, and
the possible electronic states are:
(composed mainly of Ni 4s and H 1s) will be doubly
occupied in all low lying electronic states, we are left with nine
electrons to occupy the 3d orbitals. There is thus one hole, and
the possible electronic states are: 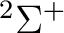 ,
, 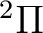 , and
, and 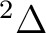 ,
depending on the orbital where the hole is located. Taking Table
,
depending on the orbital where the hole is located. Taking Table ![[*]](crossref.png) into account we observe that we have two low-lying electronic states
in symmetry 1 (A1):
into account we observe that we have two low-lying electronic states
in symmetry 1 (A1): 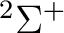 and
and 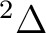 , and one in each of
the other three symmetries:
, and one in each of
the other three symmetries: 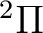 in symmetries 2 (B1) and 3 (B2),
and
in symmetries 2 (B1) and 3 (B2),
and 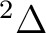 in symmetry 4 (A2). It is not immediately obvious which
of these states is the ground state as they are close in energy. It may
therefore be necessary to study all of them. It has been found at different
levels of theory that the NiH has a
in symmetry 4 (A2). It is not immediately obvious which
of these states is the ground state as they are close in energy. It may
therefore be necessary to study all of them. It has been found at different
levels of theory that the NiH has a 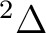 ground state [241].
ground state [241].
We continue by computing the 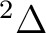 ground state. The previous SCF
orbitals will be the initial orbitals for the CASSCF calculation. First
we need to know in which C2v symmetry or symmetries we can compute
a
ground state. The previous SCF
orbitals will be the initial orbitals for the CASSCF calculation. First
we need to know in which C2v symmetry or symmetries we can compute
a 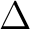 state. In the symmetry tables it is determined how the species
of the linear molecules are resolved into those of lower symmetry
(depends also on the orientation of the molecule). In Table
state. In the symmetry tables it is determined how the species
of the linear molecules are resolved into those of lower symmetry
(depends also on the orientation of the molecule). In Table ![[*]](crossref.png) is listed the assignment of the different symmetries for the molecule
placed on the z axis.
is listed the assignment of the different symmetries for the molecule
placed on the z axis.
The 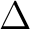 state has two degenerate components in symmetries
state has two degenerate components in symmetries 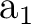 and
and 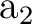 .
Two CASSCF calculations can be performed, one computing
the first root of
.
Two CASSCF calculations can be performed, one computing
the first root of 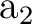 symmetry and the second for the first root of
symmetry and the second for the first root of 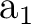 symmetry.
The RASSCF input for the state of
symmetry.
The RASSCF input for the state of 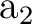 symmetry would be:
symmetry would be:
&RASSCF &END
Title
NiH 2Delta CAS s, s*, 3d, 3d'.
Symmetry
4
Spin
2
Nactel
11 0 0
Inactive
5 2 2 0
Ras2
6 2 2 2
Thrs
1.0E-07,1.0E-05,1.0E-05
Cleanup
1
4 6 10 13 18
18 1 2 3 4 5 6 7 8 9 10 11 12 16 18 19 20 21 22
4 13 14 15 17
1
1 7
10 1 2 3 4 5 6 7 8 10 11
1 9
1
1 7
10 1 2 3 4 5 6 7 9 10 11
1 8
0
Supsym
1
4 6 10 13 18
1
1 7
1
1 7
0
*Average
*1 2 3
Iter
50,25
LumOrb
End of Input
The corresponding input for symmetry 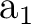 will be identical except
for the SYMMetry keyword
will be identical except
for the SYMMetry keyword
Symmetry
1
State symmetry  |
State symmetry C2v | |
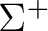 |
A1 | |
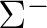 |
A2 | |
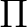 |
B1 + B2 | |
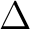 |
A1 + A2 | |
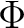 |
B1 + B2 | |
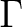 |
A1 + A2 |
In the RASSCF inputs the CLEAnup option will take the initial orbitals
(SCF here)
and will place zeroes in all the coefficients of orbitals 6, 10, 13, and 18 in symmetry 1,
except in coefficients 13, 14, 15, and 17. Likewise all coefficients 13, 14, 15, and 17
of the remaining 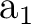 orbitals will be set to zero. The same procedure is used
in symmetries
orbitals will be set to zero. The same procedure is used
in symmetries 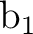 and
and 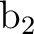 . Once cleaned, and because of the SUPSymmetry option,
the
. Once cleaned, and because of the SUPSymmetry option,
the  orbitals 6, 10, 13, and 18 of
orbitals 6, 10, 13, and 18 of 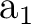 symmetry
will only rotate among themselves and they will not mix with the remaining
symmetry
will only rotate among themselves and they will not mix with the remaining
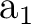
 orbitals. The same holds true for
orbitals. The same holds true for 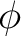 orbitals 7
orbitals 7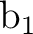 and 7
and 7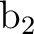 in their respective symmetries.
in their respective symmetries.
Orbitals can change order during the calculation. MOLCAS incorporates a procedure to check the nature of the orbitals in each iteration. Therefore the right behavior of the SUPSym option is guaranteed during the calculation. The procedure can have problems if the initial orbitals are not symmetrized properly. Therefore, the output with the final results should be checked to compare the final order of the orbitals and the final labeling of the SUPSym matrix.
The AVERage option would average the density matrices of symmetries 2 and 3,
corresponding to the 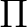 and
and 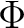 symmetries in
symmetries in 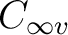 . In this case
it is not necessary to use the option because the two components of the
degenerate sets in symmetries
. In this case
it is not necessary to use the option because the two components of the
degenerate sets in symmetries 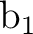 and
and 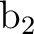 have the same occupation and
therefore they will have the same shape. The use of the option in a situation
like this (
have the same occupation and
therefore they will have the same shape. The use of the option in a situation
like this (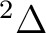 and
and 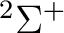 states) leads to convergence problems.
The symmetry of the orbitals in symmetries 2 and 3 is retained even if the
AVERage option is not used.
states) leads to convergence problems.
The symmetry of the orbitals in symmetries 2 and 3 is retained even if the
AVERage option is not used.
The output for the calculation on symmetry 4 (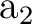 ) contains the following lines:
) contains the following lines:
Convergence after 29 iterations
30 2 2 1 -1507.59605678 -.23E-11 3 9 1 -.68E-06 -.47E-05
~
Wave function printout:
occupation of active orbitals, and spin coupling of open shells (u,d: Spin up or down)
~
printout of CI-coefficients larger than .05 for root 1
energy= -1507.596057
conf/sym 111111 22 33 44 Coeff Weight
15834 222000 20 20 u0 .97979 .95998
15838 222000 ud ud u0 .05142 .00264
15943 2u2d00 ud 20 u0 -.06511 .00424
15945 2u2d00 20 ud u0 .06511 .00424
16212 202200 20 20 u0 -.05279 .00279
16483 u220d0 ud 20 u0 -.05047 .00255
16485 u220d0 20 ud u0 .05047 .00255
~
Natural orbitals and occupation numbers for root 1
sym 1: 1.984969 1.977613 1.995456 .022289 .014882 .005049
sym 2: 1.983081 .016510
sym 3: 1.983081 .016510
sym 4: .993674 .006884
The state is mainly (weight 96%) described by a single configuration
(configuration number 15834) which placed one electron on the first active
orbital of symmetry 4 (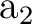 ) and the remaining electrons are paired.
A close look to this orbital indicates that is
has a coefficient -.9989 in the first 3d2- (3dxy) function and small
coefficients in the other functions. This results clearly indicate that
we have computed the
) and the remaining electrons are paired.
A close look to this orbital indicates that is
has a coefficient -.9989 in the first 3d2- (3dxy) function and small
coefficients in the other functions. This results clearly indicate that
we have computed the 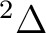 state as the lowest root of that symmetry.
The remaining configurations have negligible contributions. If the orbitals
are properly symmetrized, all configurations will be compatible with a
state as the lowest root of that symmetry.
The remaining configurations have negligible contributions. If the orbitals
are properly symmetrized, all configurations will be compatible with a
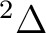 electronic state.
electronic state.
The calculation of the first root of symmetry 1 (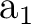 ) results:
) results:
Convergence after 15 iterations
16 2 3 1 -1507.59605678 -.19E-10 8 15 1 .35E-06 -.74E-05
~
Wave function printout:
occupation of active orbitals, and spin coupling of open shells (u,d: Spin up or down)
~
printout of CI-coefficients larger than .05 for root 1
energy= -1507.596057
conf/sym 111111 22 33 44 Coeff Weight
40800 u22000 20 20 20 -.97979 .95998
42400 u02200 20 20 20 .05280 .00279
~
Natural orbitals and occupation numbers for root 1
sym 1: .993674 1.977613 1.995456 .022289 .006884 .005049
sym 2: 1.983081 .016510
sym 3: 1.983081 .016510
sym 4: 1.984969 .014882
We obtain the same energy as in the previous calculation. Here the dominant
configuration places one electron on the first active orbital of symmetry 1 (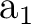 ).
It is important to remember that the orbitals are not ordered by energies or
occupations into the active space. This orbital has also the coefficient -.9989
in the first 3d2- (3dx2-y2) function. We have then computed the other
component of the
).
It is important to remember that the orbitals are not ordered by energies or
occupations into the active space. This orbital has also the coefficient -.9989
in the first 3d2- (3dx2-y2) function. We have then computed the other
component of the 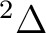 state. As the
state. As the  orbitals in different C2v symmetries are not averaged
by the program it could happen (not in the present case) that the two energies
differ slightly from each other.
orbitals in different C2v symmetries are not averaged
by the program it could happen (not in the present case) that the two energies
differ slightly from each other.
The consequences of not using the SUPSym option are not extremely severe in the present example. If you perform a calculation without the option, the obtained energy is:
Convergence after 29 iterations
30 2 2 1 -1507.59683719 -.20E-11 3 9 1 -.69E-06 -.48E-05
As it is a broken symmetry solution the energy is lower than in the other case. This is a typical behavior. If we were using an exact wave function it would have the right symmetry properties, but approximated wave functions do not necessarily fulfill this condition. So, more flexibility leads to lower energy solutions which have broken the orbital symmetry.
If in addition to the 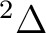 state we want to compute the lowest
state we want to compute the lowest 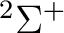 state we can use the adapted orbitals from any of the
state we can use the adapted orbitals from any of the 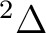 state
calculations and use the previous RASSCF input without the
CLEAnup option. The orbitals have not changed place in this example.
If they do, one has to change the labels in the SUPSym option.
The simplest way to compute the lowest excited
state
calculations and use the previous RASSCF input without the
CLEAnup option. The orbitals have not changed place in this example.
If they do, one has to change the labels in the SUPSym option.
The simplest way to compute the lowest excited 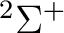 state
is having the unpaired electron in one of the
state
is having the unpaired electron in one of the  orbitals because none of
the other configurations,
orbitals because none of
the other configurations, 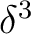 or
or 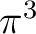 , leads to the
, leads to the 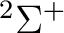 term.
However, there are more possibilities such as the configuration
term.
However, there are more possibilities such as the configuration
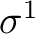
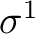
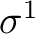 ; three nonequivalent electrons in three
; three nonequivalent electrons in three
 orbitals. In actuality
the lowest
orbitals. In actuality
the lowest 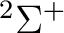 state must be computed as a doublet state in symmetry
A1. Therefore, we set the symmetry in the RASSCF to 1 and compute the second
root of the symmetry (the first was the
state must be computed as a doublet state in symmetry
A1. Therefore, we set the symmetry in the RASSCF to 1 and compute the second
root of the symmetry (the first was the 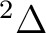 state):
state):
CIRoot
1 2
2
Of course the SUPSym option must be maintained. The use of CIROot indicates that we are computing the second root of that symmetry. The obtained result:
Convergence after 33 iterations
9 2 3 2 -1507.58420263 -.44E-10 2 11 2 -.12E-05 .88E-05
~
Wave function printout:
occupation of active orbitals, and spin coupling of open shells (u,d: Spin up or down)
~
printout of CI-coefficients larger than .05 for root 1
energy= -1507.584813
conf/sym 111111 22 33 44 Coeff Weight
40800 u22000 20 20 20 -.97917 .95877
~
printout of CI-coefficients larger than .05 for root 2
energy= -1507.584203
conf/sym 111111 22 33 44 Coeff Weight
40700 2u2000 20 20 20 .98066 .96169
~
Natural orbitals and occupation numbers for root 2
sym 1: 1.983492 .992557 1.995106 .008720 .016204 .004920
sym 2: 1.983461 .016192
sym 3: 1.983451 .016192
sym 4: 1.983492 .016204
As we have used two as the dimension of the CI matrix employed in the CI Davidson
procedure we obtain the wave function of two roots, although the optimized
root is the second. Root 1 places one electron in the first active orbital
of symmetry one, which is a 3d2+ (3dx2-y2)  orbital. Root 2 places
the electron in the second active orbital, which is a
orbital. Root 2 places
the electron in the second active orbital, which is a  orbital with a
large coefficient (.9639) in the first 3d0 (3dz2) function of the nickel
atom. We have therefore computed the lowest
orbital with a
large coefficient (.9639) in the first 3d0 (3dz2) function of the nickel
atom. We have therefore computed the lowest 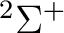 state. The two
state. The two 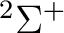 states
resulting from the configuration with the three unpaired
states
resulting from the configuration with the three unpaired  electrons
is higher in energy at the CASSCF level. If the second root of symmetry
electrons
is higher in energy at the CASSCF level. If the second root of symmetry 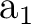 had not been a
had not been a 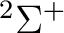 state we would have to study higher roots of the
same symmetry.
state we would have to study higher roots of the
same symmetry.
It is important to remember that the active orbitals are not ordered at all within the active space. Therefore, their order might vary from calculation to calculation and, in addition, no conclusions about the orbital energy, occupation or any other information can be obtained from the order of the active orbitals.
We can compute also the lowest 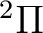 excited state.
The simplest possibility is having the configuration
excited state.
The simplest possibility is having the configuration 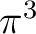 ,
which only leads to one
,
which only leads to one 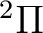 state. The unpaired electron
will be placed in either one
state. The unpaired electron
will be placed in either one 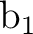 or one
or one 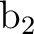 orbital. That means
that the state has two degenerate components and we can compute it
equally in both symmetries. There are more possibilities, such as the
configuration
orbital. That means
that the state has two degenerate components and we can compute it
equally in both symmetries. There are more possibilities, such as the
configuration
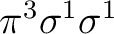 or the configuration
or the configuration
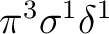 .
The resulting
.
The resulting 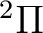 state will always have two degenerate
components in symmetries
state will always have two degenerate
components in symmetries
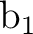 and
and 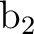 , and therefore it is the wave function analysis which
gives us the information of which configuration leads to
the lowest
, and therefore it is the wave function analysis which
gives us the information of which configuration leads to
the lowest 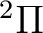 state.
state.
For NiH it turns out to be non trivial to compute the 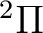 state.
Taking as initial orbitals
the previous SCF orbitals and using any type of restriction such as
the CLEAnup, SUPSym or AVERage options lead to
severe convergence problems like these:
state.
Taking as initial orbitals
the previous SCF orbitals and using any type of restriction such as
the CLEAnup, SUPSym or AVERage options lead to
severe convergence problems like these:
45 9 17 1 -1507.42427683 -.65E-02 6 18 1 -.23E-01 -.15E+00
46 5 19 1 -1507.41780710 .65E-02 8 15 1 .61E-01 -.15E+00
47 9 17 1 -1507.42427683 -.65E-02 6 18 1 -.23E-01 -.15E+00
48 5 19 1 -1507.41780710 .65E-02 8 15 1 .61E-01 -.15E+00
49 9 17 1 -1507.42427683 -.65E-02 6 18 1 -.23E-01 -.15E+00
50 5 19 1 -1507.41780710 .65E-02 8 15 1 .61E-01 -.15E+00
~
No convergence after 50 iterations
51 9 19 1 -1507.42427683 -.65E-02 6 18 1 -.23E-01 -.15E+00
The calculation, however, converges in an straightforward way if none of those tools are used:
Convergence after 33 iterations
34 2 2 1 -1507.58698677 -.23E-12 3 8 2 -.72E-06 -.65E-05
~
Wave function printout:
occupation of active orbitals, and spin coupling of open shells (u,d: Spin up or down)
~
printout of CI-coefficients larger than .05 for root 1
energy= -1507.586987
conf/sym 111111 22 33 44 Coeff Weight
15845 222000 u0 20 20 .98026 .96091
15957 2u2d00 u0 ud 20 .05712 .00326
16513 u220d0 u0 20 ud -.05131 .00263
~
Natural orbitals and occupation numbers for root 1
sym 1: 1.984111 1.980077 1.995482 .019865 .015666 .004660
sym 2: .993507 .007380
sym 3: 1.982975 .016623
sym 4: 1.983761 .015892
The 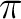 (and
(and 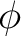 ) orbitals, both in symmetries
) orbitals, both in symmetries 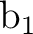 and
and 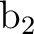 , are, however,
differently occupied and therefore are not equal as they should be:
, are, however,
differently occupied and therefore are not equal as they should be:
Molecular orbitals for sym species 2 Molecular orbitals for symmetry species 3
ORBITAL 3 4 ORBITAL 3 4
ENERGY .0000 .0000 ENERGY .0000 .0000
OCC. NO. .9935 .0074 OCC. NO. 1.9830 .0166
~
1 NI 2px .0001 .0002 1 NI 2py .0018 -.0001
2 NI 2px .0073 .0013 2 NI 2py .0178 -.0002
3 NI 2px -.0155 .0229 3 NI 2py -.0197 -.0329
4 NI 2px .0041 .0227 4 NI 2py .0029 -.0254
5 NI 3d1+ .9990 -.0199 5 NI 3d1- .9998 -.0131
6 NI 3d1+ -.0310 -.8964 6 NI 3d1- .0128 .9235
7 NI 3d1+ -.0105 .4304 7 NI 3d1- .0009 -.3739
8 NI 4f1+ -.0050 .0266 8 NI 4f3- .0001 -.0003
9 NI 4f3+ .0001 .0000 9 NI 4f1- -.0050 -.0177
10 H 2px .0029 -.0149 10 H 2py .0009 .0096
11 H 2px -.0056 -.0003 11 H 2py -.0094 -.0052
Therefore what we have is a symmetry broken solution. To obtain a solution which
is not of broken nature the 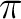 and
and 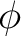 orbitals must be equivalent.
The tool to obtain equivalent orbitals is the AVERage option, which averages
the density matrices of symmetries
orbitals must be equivalent.
The tool to obtain equivalent orbitals is the AVERage option, which averages
the density matrices of symmetries 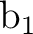 and
and 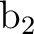 . But starting with any of the preceding
orbitals and using the AVERage option lead again to convergence problems.
It is necessary to use better initial orbitals; orbitals which have
already equal orbitals in symmetries
. But starting with any of the preceding
orbitals and using the AVERage option lead again to convergence problems.
It is necessary to use better initial orbitals; orbitals which have
already equal orbitals in symmetries 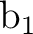 and
and 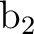 . One possibility is to perform a
SCF calculation on the NiH cation explicitly indicating occupation one in the two
higher occupied
. One possibility is to perform a
SCF calculation on the NiH cation explicitly indicating occupation one in the two
higher occupied 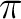 orbitals (symmetries 2 and 3):
orbitals (symmetries 2 and 3):
&SCF &END
TITLE
NiH cation
OCCUPIED
8 3 3 1
OCCNO
2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0
2.0 2.0 1.0 <-- Note the extra occupation
2.0 2.0 1.0 <-- Note the extra occupation
2.0
IVO
END OF INPUT
It can take some successive steps to obtain a converged calculation using the
CLEAnup, SUPSym, and AVERage options. The calculation
with a single root did not converge clearly. We obtained, however, a converged
result for the lowest 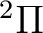 state of NiH
by computing two averaged CASSCF roots and setting a weight of
90% for the first root using the keyword:
state of NiH
by computing two averaged CASSCF roots and setting a weight of
90% for the first root using the keyword:
CIROot
2 2
1 2
9 1
~
Wave function printout:
occupation of active orbitals, and spin coupling of open shells (u,d: Spin up or down)
~
printout of CI-coefficients larger than .05 for root 1
energy= -1507.566492
conf/sym 111111 22 33 44 Coeff Weight
4913 222u00 20 d0 u0 -.05802 .00337
15845 222000 u0 20 20 .97316 .94703
15953 2u2d00 u0 20 20 .05763 .00332
16459 2u20d0 u0 20 ud -.05283 .00279
~
Natural orbitals and occupation numbers for root 1
sym 1: 1.972108 1.982895 1.998480 .028246 .016277 .007159
sym 2: .997773 .007847
sym 3: 1.978019 .016453
sym 4: 1.978377 .016366
The energy of the different states (only the first one shown above) is
printed on the top of their configuration list. The converged energy is
simply an average energy.
The occupation numbers obtained in the section of the RASSCF output printed
above are the occupation numbers of the natural orbitals of the corresponding
root. They differ from the occupation numbers printed in the
molecular orbital section where we have pseudonatural molecular orbitals and
average occupation numbers. On top of each of the valence 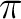 orbitals
an average occupation close to 1.5e will be printed; this is a consequence
of the the averaging procedure.
orbitals
an average occupation close to 1.5e will be printed; this is a consequence
of the the averaging procedure.
The results obtained are only at the CASSCF level. Additional effects have to be considered and included. The most important of them is the dynamical correlation effect which can be added by computing, for instance, the CASPT2 energies. The reader can find a detailed explanation of the different approaches in ref. [241], and a careful discussion of their consequences and solutions in ref. [244].
We are going, however, to point out some details. In the first place the basis set
must include up to g functions for the transition metal atom and up to d
functions for the hydrogen. Relativistic effects must be taken into account,
at least in a simple way as a first order correction. The keyword RELInt
must be then included in the SEWARD input to compute the mass-velocity and
one-electron Darwin contact term integrals and obtain a first-order correction
to the energy with respect to relativistic effects at the CASSCF level in the RASSCF output.
Scalar relativistic effects can be also included according the Douglas-Kroll
or the Barysz-Sadlej-Snijders transformations, as it will be explained in
section ![[*]](crossref.png) .
.
The CASPT2 input needed to compute the second-order correction to the energy will include the number of the CASSCF root to compute. For instance, for the first root of each symmetry:
&CASPT2 &END
Title
NiH
Frozen
5 2 2 0
Maxit
30
Lroot
1
End of input
The number of frozen orbitals taken by CASPT2 will be that specified in the RASSCF input except if this is changed in the CASPT2 input. In the perturbative step we have frozen all the occupied orbitals except the active ones. This is motivated by the desire to include exclusively the dynamical correlation related to the valence electrons. In this way we neglect correlation between core electrons, named core-core correlation, and between core and valence electrons, named core-valence correlation. This is not because the calculation is smaller but because of the inclusion of those type of correlation in a calculation designed to treat valence correlation is an inadequate approach. Core-core and core-valence correlation requires additional basis functions of the same spatial extent as the occupied orbitals being correlated, but with additional radial and angular nodes. Since the spatial extent of the core molecular orbitals is small, the exponents of these correlating functions must be much larger than those of the valence optimized basis sets. The consequence is that we must avoid the inclusion of the core electrons in the treatment in the first step. Afterwards, the amount of correlation introduced by the core electrons can be estimated in separated calculations for the different states and those effects added to the results with the valence electrons.
Core-valence correlation effects of the 3s and 3p nickel shells can be studied by increasing the basis set flexibility by uncontracting the basis set in the appropriate region. There are different possibilities. Here we show the increase of the basis set by four s, four p, and four d functions. f functions contribute less to the description of the 3s and 3p shells and can be excluded. The uncontracted exponents should correspond to the region where the 3s and 3p shells present their density maximum. Therefore, first we compute the absolute maxima of the radial distribution of the involved orbitals, then we determine the primitive gaussian functions which have their maxima in the same region as the orbitals and therefore which exponents should be uncontracted. The final basis set will be the valence basis set used before plus the new added functions. In the present example the SEWARD input can be:
&SEWARD &END
Title
NiH G.S.
Symmetry
X Y
*RelInt
Basis set
Ni.ANO-L...5s4p3d1f.
Ni 0.00000 0.00000 0.000000 Bohr
End of basis
Basis set
Ni....4s4p4d. / Inline
0. 2
* Additional s functions
4 4
3.918870 1.839853 0.804663 0.169846
1. 0. 0. 0.
0. 1. 0. 0.
0. 0. 1. 0.
0. 0. 0. 1.
* Additional p functions
4 4
2.533837 1.135309 0.467891 0.187156
1. 0. 0. 0.
0. 1. 0. 0.
0. 0. 1. 0.
0. 0. 0. 1.
* Additional d functions
4 4
2.551303 1.128060 0.475373 0.182128
1. 0. 0. 0.
0. 1. 0. 0.
0. 0. 1. 0.
0. 0. 0. 1.
Nix 0.00000 0.00000 0.000000 Bohr
End of basis
Basis set
H.ANO-L...3s2p.
H 0.000000 0.000000 2.747000 Bohr
End of basis
End of Input
We have used a special format to include the additional functions. We include the additional 4s4p4d functions for the nickel atom. The additional basis set input must use a dummy label (Nix here), the same coordinates of the original atom, and specify a CHARge equal to zero, whether in an Inline basis set input as here or by specifically using keyword CHARge. It is not necessary to include the basis set with the Inline format. A library can be created for this purpose. In this case the label for the additional functions could be:
Ni.Uncontracted...4s4p4d. / AUXLIB
Charge
0
and a proper link to AUXLIB should be included in the script (or in the input if one uses AUTO).
Now the CASPT2 is going to be different to include also the correlation related to the 3s,3p shell of the nickel atom. Therefore, we only freeze the 1s,2s,2p shells:
&CASPT2 &END
Title
NiH. Core-valence.
Frozen
3 1 1 0
Maxit
30
Lroot
1
End of input
A final effect one should study is the basis set superposition error (BSSE). In many cases it is a minor effect but it is an everpresent phenomenon which should be investigated when high accuracy is required, especially in determining bond energies, and not only in cases with weakly interacting systems, as is frequently believed. The most common approach to estimate this effect is the counterpoise correction: the separated fragment energies are computed in the total basis set of the system. For a discussion of this issue see Refs. [244,245]. In the present example we would compute the energy of the isolated nickel atom using a SEWARD input including the full nickel basis set plus the hydrogen basis set in the hydrogen position but with the charge set to zero. And then the opposite should be done to compute the energy of isolated hydrogen. The BSSE depends on the separation of the fragments and must be estimated at any computed geometry. For instance, the SEWARD input necessary to compute the isolated hydrogen atom at a given distance from the ghost nickel basis set including core uncontracted functions is:
>>UNIX mkdir AUXLIB
>>COPY $CurrDir/NiH.NewLib AUXLIB/UNCONTRACTED
&SEWARD &END
Title
NiH. 3s3p + H (BSSE)
Symmetry
X Y
RelInt
Basis set
Ni.ANO-L...5s4p3d1f.
Ni 0.00000 0.00000 0.000000 Bohr
Charge
0.0
End of basis
Basis set
Ni.Uncontracted...4s4p4d. / AUXLIB
Nix 0.00000 0.00000 0.000000 Bohr
Charge
0.0
End of basis
Basis set
H.ANO-L...3s2p.
H 0.000000 0.000000 2.747000 Bohr
End of basis
End of Input
Once the energy of each of the fragments with the corresponding ghost
basis set of the other fragment is determined, the energies of the
completely isolated fragments can be computed and subtracted from those
which have the ghost basis sets. Other approaches used to estimate
the BSSE effect are discussed in Ref. [244].
The results obtained at the CASPT2 level are close to those obtained by MRCI+Q and ACPF treatments but more accurate. They match well with experiment. The difference is that all the configuration functions (CSFs) of the active space can be included in CASPT2 in the zeroth-order references for the second-order perturbation calculation [241], while the other methods have to restrict the number of configurations.
Calculations of linear molecules become more and more complicated when the number of unpaired electrons increases. In the following sections we will discuss the more complicated situation occurring in the Ni2 molecule.
10.1.2 A diatomic homonuclear molecule: C2
C2 is a classical example of a system where near-degeneracy effects have large
amplitudes even near the equilibrium internuclear separation. The biradical
character of the ground state of the molecule suggest that a single
configurational treatment will not be appropriate for accurate descriptions
of the spectroscopic constants [85].
There are two nearly degenerate states: 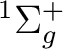 and
and 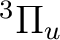 . The latter
was earlier believed to be the ground state, an historical assignment which can
be observed in the traditional labeling of the states.
. The latter
was earlier believed to be the ground state, an historical assignment which can
be observed in the traditional labeling of the states.
As C2 is a 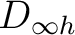 molecule, we have to compute it in D2h symmetry. We
make a similar analysis as for the C2v case. We begin by
classifying the functions in
molecule, we have to compute it in D2h symmetry. We
make a similar analysis as for the C2v case. We begin by
classifying the functions in 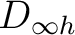 in Table
in Table ![[*]](crossref.png) .
The molecule is placed on the z axis.
.
The molecule is placed on the z axis.
| Symmetry | Spherical harmonics | |||
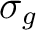 |
s | dz2 | ||
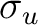 |
pz | fz3 | ||
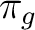 |
dxz | dyz | ||
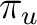 |
px | py | fx(z2-y2) | fy(z2-x2) |
 |
dx2-y2 | dxy | ||
 |
fxyz | fz(x2-y2) | ||
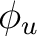 |
fx3 | fy3 | ||
| aFunctions placed on the symmetry center. | ||||
Table ![[*]](crossref.png) classifies
the functions and orbitals into the symmetry representations of the D2h symmetry. Note that in table
classifies
the functions and orbitals into the symmetry representations of the D2h symmetry. Note that in table ![[*]](crossref.png) subindex b stands for bonding combination and
a for antibonding combination.
subindex b stands for bonding combination and
a for antibonding combination.
| Symm.b | Spherical harmonics (orbitals in 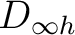 ) ) |
|||||
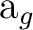 (1) (1) |
sb (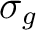 ) ) |
pzb (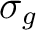 ) ) |
dz2b (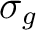 ) ) |
dx2-y2b ( ) ) |
fz3b (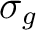 ) ) |
fz(x2-y2)b ( ) ) |
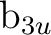 (2) (2) |
pxb (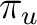 ) ) |
dxzb (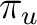 ) ) |
fx(z2-y2)b (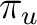 ) ) |
fx3b (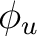 ) ) |
||
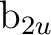 (3) (3) |
pyb (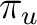 ) ) |
dyzb (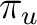 ) ) |
fy(z2-x2)b (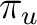 ) ) |
fy3b (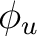 ) ) |
||
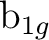 (4) (4) |
dxyb ( ) ) |
fxyzb ( ) ) |
||||
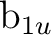 (5) (5) |
sa (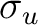 ) ) |
pza (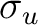 ) ) |
dz2a (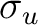 ) ) |
dx2-y2a ( ) ) |
fz3a (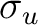 ) ) |
fz(x2-y2)a ( ) ) |
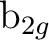 (6) (6) |
pya (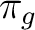 ) ) |
dyza (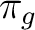 ) ) |
fy(z2-x2)a (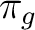 ) ) |
fy3a (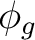 ) ) |
||
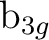 (7) (7) |
pxa (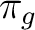 ) ) |
dxza (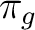 ) ) |
fx(z2-y2)a (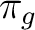 ) ) |
fx3a (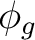 ) ) |
||
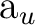 (8) (8) |
dxya ( ) ) |
fxyza ( ) ) |
||||
| aSubscripts a and b refer to the bonding and antibonding combination of the AO's, respectively. | ||||||
| bIn parenthesis the number of the symmetry in MOLCAS. Note that the number and order of the | ||||||
| symmetries depend on the generators and the orientation of the molecule. | ||||||
The order of the symmetries, and therefore the number they have in MOLCAS, depends
on the generators used in the SEWARD input. This must be carefully checked
at the beginning of any calculation. In addition, the orientation of the molecule on the
cartesian axis can change the labels of the symmetries. In Table ![[*]](crossref.png) for
instance we have used the order and numbering of a calculation performed with the
three symmetry planes of the D2h point group (X Y Z in the SEWARD input)
and the z axis as the intermolecular axis (that is, x and y are equivalent in D2h).
Any change in the orientation of the molecule will affect the labels of the orbitals
and states. In this case the
for
instance we have used the order and numbering of a calculation performed with the
three symmetry planes of the D2h point group (X Y Z in the SEWARD input)
and the z axis as the intermolecular axis (that is, x and y are equivalent in D2h).
Any change in the orientation of the molecule will affect the labels of the orbitals
and states. In this case the 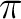 orbitals will belong to the
orbitals will belong to the 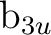 ,
, 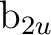 ,
,
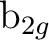 , and
, and 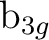 symmetries. For instance, with x as the intermolecular axis
symmetries. For instance, with x as the intermolecular axis 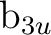 and
and 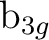 will
be replaced by
will
be replaced by 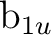 and
and 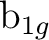 , respectively, and finally with y as the intermolecular axis
, respectively, and finally with y as the intermolecular axis
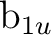 ,
, 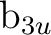 ,
, 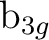 , and
, and 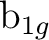 would be the
would be the 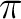 orbitals.
orbitals.
It is important to remember that MOLCAS works with symmetry adapted basis functions. Only the symmetry independent atoms are required in the SEWARD input. The remaining ones will be generated by the symmetry operators. This is also the case for the molecular orbitals. MOLCAS will only print the coefficients of the symmetry adapted basis functions.
The necessary information to obtain the complete set of orbitals
is contained in the SEWARD output. Consider the case of the 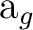 symmetry:
symmetry:
**************************************************
******** Symmetry adapted Basis Functions ********
**************************************************
~
Irreducible representation : ag
Basis function(s) of irrep:
~
Basis Label Type Center Phase Center Phase
1 C 1s0 1 1 2 1
2 C 1s0 1 1 2 1
3 C 1s0 1 1 2 1
4 C 1s0 1 1 2 1
5 C 2pz 1 1 2 -1
6 C 2pz 1 1 2 -1
7 C 2pz 1 1 2 -1
8 C 3d0 1 1 2 1
9 C 3d0 1 1 2 1
10 C 3d2+ 1 1 2 1
11 C 3d2+ 1 1 2 1
12 C 4f0 1 1 2 -1
13 C 4f2+ 1 1 2 -1
The previous output indicates that symmetry adapted basis function 1,
belonging to the 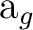 representation, is formed by
the symmetric combination of a s type function centered on atom C and
another s type function centered on the redundant center 2, the second
carbon atom. Combination s+s constitutes a bonding
representation, is formed by
the symmetric combination of a s type function centered on atom C and
another s type function centered on the redundant center 2, the second
carbon atom. Combination s+s constitutes a bonding 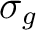 -type
orbital. For the pz function however the combination must be
antisymmetric. It is the only way to make the pz orbitals overlap
and form a bonding orbital of
-type
orbital. For the pz function however the combination must be
antisymmetric. It is the only way to make the pz orbitals overlap
and form a bonding orbital of 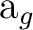 symmetry. Similar combinations are obtained for the
remaining basis sets of the
symmetry. Similar combinations are obtained for the
remaining basis sets of the 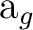 and other symmetries.
and other symmetries.
The molecular orbitals will be combinations of these symmetry adapted
functions. Consider the 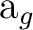 orbitals:
orbitals:
SCF orbitals
~
Molecular orbitals for symmetry species 1
~
ORBITAL 1 2 3 4 5 6
ENERGY -11.3932 -1.0151 -.1138 .1546 .2278 .2869
OCC. NO. 2.0000 2.0000 .0098 .0000 .0000 .0000
~
1 C 1s0 1.4139 -.0666 -.0696 .2599 .0626 .0000
2 C 1s0 .0003 1.1076 -.6517 1.0224 .4459 .0000
3 C 1s0 .0002 -.0880 -.2817 .9514 .0664 .0000
4 C 1s0 .0000 -.0135 -.0655 .3448 -.0388 .0000
5 C 2pz -.0006 -.2581 -1.2543 1.1836 .8186 .0000
6 C 2pz .0000 .1345 -.0257 2.5126 1.8556 .0000
7 C 2pz .0005 -.0192 -.0240 .7025 .6639 .0000
8 C 3d0 .0003 .0220 -.0005 -.9719 .2430 .0000
9 C 3d0 -.0001 -.0382 -.0323 -.8577 .2345 .0000
10 C 3d2+ .0000 .0000 .0000 .0000 .0000 -.7849
11 C 3d2+ .0000 .0000 .0000 .0000 .0000 -.7428
12 C 4f0 -.0002 -.0103 -.0165 .0743 .0081 .0000
13 C 4f2+ .0000 .0000 .0000 .0000 .0000 -.0181
In MOLCAS outputs only 13 coefficients for orbital are going to be printed because they are the coefficients of the symmetry adapted basis functions. If the orbitals were not composed by symmetry adapted basis functions they would have, in this case, 26 coefficients, two for type of function (following the scheme observed above in the SEWARD output), symmetrically combined the s and d functions and antisymmetrically combined the p and f functions.
To compute 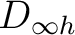 electronic states using the D2h symmetry we need
to go to the symmetry tables and determine how the species
of the linear molecules are resolved into those of lower symmetry
(this depends also on the orientation of the molecule [243]).
Table
electronic states using the D2h symmetry we need
to go to the symmetry tables and determine how the species
of the linear molecules are resolved into those of lower symmetry
(this depends also on the orientation of the molecule [243]).
Table ![[*]](crossref.png) lists the case of a
lists the case of a 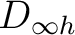 linear molecule with z as
the intermolecular axis.
linear molecule with z as
the intermolecular axis.
State symmetry 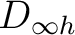 |
State symmetry D2h | |
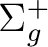 |
Ag | |
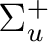 |
B1u | |
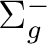 |
B1g | |
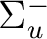 |
Au | |
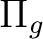 |
B2g + B3g | |
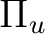 |
B2u + B3u | |
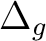 |
Ag + B1g | |
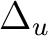 |
Au + B1u | |
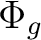 |
B2g + B3g | |
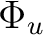 |
B2u + B3u | |
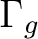 |
Ag + B1g | |
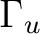 |
Au + B1u |
To compute the ground state of C2, a 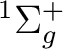 state, we will
compute a singlet state of symmetry Ag (1 in this context).
The input files for a CASSCF calculation on the C2 ground state
will be:
state, we will
compute a singlet state of symmetry Ag (1 in this context).
The input files for a CASSCF calculation on the C2 ground state
will be:
&SEWARD &END
Title
C2
Symmetry
X Y Z
Basis set
C.ANO-L...4s3p2d1f.
C .00000000 .00000000 1.4
End of basis
End of input
&SCF &END
Title
C2
ITERATIONS
40
Occupied
2 1 1 0 2 0 0 0
End of input
&RASSCF &END
Title
C2
Nactel
4 0 0
Spin
1
Symmetry
1
Inactive
2 0 0 0 2 0 0 0
Ras2
1 1 1 0 1 1 1 0
*Average
*2 2 3 6 7
Supsymmetry
1
3 6 9 11
1
1 6
1
1 6
0
1
3 5 8 12
1
1 6
1
1 6
0
Iter
50,25
Lumorb
End of input
In this case the SCF orbitals are already clean symmetry adapted orbitals
(within the printed accuracy).
We can then directly use the SUPSym option. In symmetries
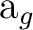 and
and 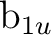 we restrict the rotations among the
we restrict the rotations among the  and
the
and
the  orbitals, and in symmetries
orbitals, and in symmetries 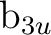 ,
, 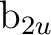 ,
, 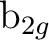 , and
, and
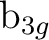 the rotations among
the rotations among 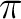 and
and 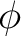 orbitals. Additionally,
symmetries
orbitals. Additionally,
symmetries 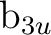 and
and 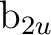 and symmetries
and symmetries 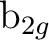 and
and
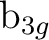 are averaged, respectively, by using
the AVERage option. They belong to the
are averaged, respectively, by using
the AVERage option. They belong to the 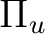 and
and
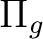 representations in
representations in 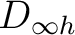 , respectively.
, respectively.
A detailed explanation on different CASSCF calculations on the C2 molecule and their states can be found elsewhere [85]. Instead we include here an example of how to combine the use of UNIX shell script commands with MOLCAS as a powerful tool.
The following example computes the transition dipole moment for the transition
from the 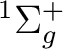 state to the
state to the 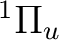 state in the C2
molecule. This transition is known as the Phillips bands [243].
This is not a serious attempt to compute this property accurately, but serves
as an example of how to set up an automatic calculation.
The potential curves are computed using CASSCF wavefunctions
along with the transition dipole moment.
state in the C2
molecule. This transition is known as the Phillips bands [243].
This is not a serious attempt to compute this property accurately, but serves
as an example of how to set up an automatic calculation.
The potential curves are computed using CASSCF wavefunctions
along with the transition dipole moment.
Starting orbitals are generated by computing a CI wavefunction once and using the natural orbitals. We loop over a set of distances, compute the CASSCF wave functions for both states and use RASSI to compute the TDMs. Several UNIX commands are used to manipulate input and output files, such as grep, sed, and the awk language. For instance, an explicit 'sed' is used to insert the geometry into the seward input; the final CASSCF energy is extracted with an explicit 'grep', and the TDM is extracted from the RASSI output using an awk script. We are not going to include the awk scripts here. Other tools can be used to obtain and collect the data.
In the first script, when the loop over geometries is done, four files are available:
geom.list (contains the distances), tdm.list (contains the TDMs),
e1.list (contains the energy for the 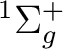 state), and
e2.list (contains the energy for the
state), and
e2.list (contains the energy for the 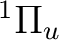 state). In the second script the vibrational
wave functions for the two states and the vibrationally averaged TDMs
are now computed using the VIBROT program. We will retain the RASSCF outputs
in the scratch directory to check the wave function. It is always dangerous
to assume that the wave functions will be correct in a CASSCF calculation.
Different problems such as root flippings or incorrect orbitals rotating into the
active space are not uncommon. Also, it is always necessary to control that the
CASSCF calculation has converged. The first script (Korn shell) is:
state). In the second script the vibrational
wave functions for the two states and the vibrationally averaged TDMs
are now computed using the VIBROT program. We will retain the RASSCF outputs
in the scratch directory to check the wave function. It is always dangerous
to assume that the wave functions will be correct in a CASSCF calculation.
Different problems such as root flippings or incorrect orbitals rotating into the
active space are not uncommon. Also, it is always necessary to control that the
CASSCF calculation has converged. The first script (Korn shell) is:
#!/bin/ksh
#
# perform some initializations
#
export Project='C2'
export WorkDir=/temp/$LOGNAME/$Project
export Home=/u/$LOGNAME/$Project
echo "No log" > current.log
trap 'cat current.log ; exit 1' ERR
mkdir $WorkDir
cd $WorkDir
#
# Loop over the geometries and generate input for vibrot
#
list="1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 5.0 10.0"
scf='yes'
print "Sigma" > e1.list
print "Pi" > e2.list
for geom in $list
do
#--- run seward
print "Dist $geom" >> geom.list
sed -e "s/#/$geom/" $Home/$Project.seward.input > seward.input
molcas seward.input > current.log
#--- optionally run scf, motra, guga and mrci to obtain good starting orbitals
if [ "$scf" = 'yes' ]
then
scf='no'
molcas $Home/$Project.scf.input > current.log
molcas $Home/$Project.motra.input > current.log
molcas $Home/$Project.guga.input > current.log
molcas $Home/$Project.mrci.input > current.log
cp $Project.CiOrb $Project.RasOrb1
cp $Project.CiOrb $Project.RasOrb2
fi
#--- rasscf wavefunction for 1Sg+
ln -fs $Project.Job001 JOBIPH
ln -fs $Project.RasOrb1 INPORB
molcas $Home/$Project.rasscf1.input > current.log
cat current.log >> rasscf1.log
cat current.log | grep -i 'average ci' >> e1.list
cp $Project.RasOrb $Project.RasOrb1
rm -f JOBIPH INPORB
#--- rasscf wavefunction for 1Pu
ln -fs $Project.Job002 JOBIPH
ln -fs $Project.RasOrb2 INPORB
molcas $Home/$Project.rasscf2.input > current.log
cat current.log >> rasscf2.log
cat current.log | grep -i 'average ci' >> e2.list
cp $Project.RasOrb $Project.RasOrb2
rm -f JOBIPH INPORB
#--- rassi to obtain transition
ln -fs $Project.Job001 JOB001
ln -fs $Project.Job002 JOB002
molcas $Home/$Project.rassi.input > current.log
awk -f $Home/tdm.awk current.log >> tdm.list
rm -f JOB001 JOB002
#---
done
#
# Finished so clean up the files.
#
print "Calculation finished" >&2
cd -
rm $WorkDir/molcas.temp*
#rm -r $WorkDir
exit 0
In a second script we will compute the vibrational wave functions
#!/bin/ksh
#
# perform some initializations
#
export Project='C2'
export WorkDir=/temp/$LOGNAME/$Project
export Home=/u/$LOGNAME/$Project
echo "No log" > current.log
trap 'cat current.log ; exit 1' ERR
mkdir $WorkDir
cd $WorkDir
#
# Build vibrot input
#
cp e1.list $Home
cp e2.list $Home
cp geom.list $Home
cp tdm.list $Home
#---
cat e1.list geom.list | awk -f $Home/wfn.awk > vibrot1.input
cat e2.list geom.list | awk -f $Home/wfn.awk > vibrot2.input
cat tdm.list geom.list | awk -f $Home/tmc.awk > vibrot3.input
#---
ln -fs $Project.VibWvs1 VIBWVS
molcas vibrot1.input > current.log
cat current.log
rm -f VIBWVS
#---
ln -fs $Project.VibWvs2 VIBWVS
molcas vibrot2.input > current.log
cat current.log
rm -f VIBWVS
#---
ln -fs $Project.VibWvs1 VIBWVS1
ln -fs $Project.VibWvs2 VIBWVS2
molcas vibrot3.input > current.log
cat current.log
rm -f VIBWVS1 VIBWVS2
#
# Finished so clean up the files.
#
print "Calculation finished" >&2
cd -
rm $WorkDir/molcas.temp*
#rm -r $WorkDir
exit 0
The input for the first part of the calculations include the SEWARD, SCF, MOTRA, GUGA, and MRCI inputs:
&SEWARD &END
Title
C2
Pkthre
1.0D-11
Symmetry
X Y Z
Basis set
C.ANO-S...3s2p.
C .00000000 .00000000 #
End of basis
End of input
&SCF &END
Title
C2
ITERATIONS
40
Occupied
2 1 1 0 2 0 0 0
End of input
&MOTRA &END
Title
C2 molecule
Frozen
1 0 0 0 1 0 0 0
LumOrb
End of input
&GUGA &END
Title
C2 molecule
Electrons
8
Spin
1
Inactive
1 1 1 0 1 0 0 0
Active
0 0 0 0 0 0 0 0
CiAll
1
End of Input
&MRCI &END
Title
C2 molecule
SDCI
End of input
We are going to use a small ANO [3s2p] basis set because our purpose it is not to obtain an extreme accuracy. In the SEWARD input the sign '#' will be replaced by the right distance using the 'sed' command. In the MOTRA input we have frozen the two core orbitals in the molecule, which will be recognized by the MRCI program. The GUGA input defines the reference space of configurations for the subsequent MRCI or ACPF calculation. In this case the valence orbitals are doubly occupied and there is only one reference configuration (they are included as inactive). We thus use one single configuration to perform the SDCI calculation and obtain the initial set of orbitals for the CASSCF calculation.
The lowest 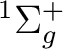 state in C2 is the result of the
electronic configuration [core](2
state in C2 is the result of the
electronic configuration [core](2 )2 (2
)2 (2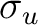 )2
(1
)2
(1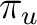 )4. Only one electronic state is obtained from this
configuration. The configuration (1
)4. Only one electronic state is obtained from this
configuration. The configuration (1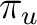 )3 (3
)3 (3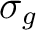 )1
is close in energy and generates two possibilities,
one
)1
is close in energy and generates two possibilities,
one 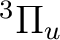 and one
and one 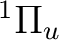 state. The former is the lowest
state of the Swan bands, and was thought to be the ground state of
the molecule. Transitions to the
state. The former is the lowest
state of the Swan bands, and was thought to be the ground state of
the molecule. Transitions to the 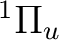 state are known as the
Phillips band and this is the state we are going to compute.
We have the possibility to compute the state in symmetry
state are known as the
Phillips band and this is the state we are going to compute.
We have the possibility to compute the state in symmetry 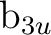 or
or
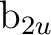 ( MOLCAS symmetry groups 2 and 3, respectively ) in the D2h
group, because both represent the degenerate
( MOLCAS symmetry groups 2 and 3, respectively ) in the D2h
group, because both represent the degenerate 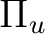 symmetry in
symmetry in 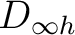 .
.
The RASSCF input file to compute the two states are:
&RASSCF &END
Title
C2 1Sigmag+ state.
Nactel
4 0 0
Spin
1
Symmetry
1
Inactive
2 0 0 0 2 0 0 0
Ras2
1 1 1 0 1 1 1 0
*Average
*2 2 3 6 7
OutOrbitals
Natural
1
Iter
50,25
Lumorb
End of input
&RASSCF &END
Title
C2 1Piu state.
Nactel
4 0 0
Spin
1
Symmetry
2
Inactive
2 0 0 0 2 0 0 0
Ras2
1 1 1 0 1 1 1 0
Average
2 2 3 6 7
OutOrbitals
Natural
1
Iter
50,25
Lumorb
End of input
We can skip the SUPSym option because our basis set
contains only s,p functions and no undesired rotations can
happen. Symmetries 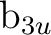 and
and 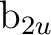 on one hand and
on one hand and 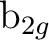 and
and 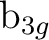 on
the other are averaged. Notice that to obtain natural orbitals we have
used keyword OUTOrbitals instead of the old RASREAD
program. In addition, we need the RASSI input:
on
the other are averaged. Notice that to obtain natural orbitals we have
used keyword OUTOrbitals instead of the old RASREAD
program. In addition, we need the RASSI input:
&RASSI &END
NrOfJobiphs
2 1 1
1
1
End of input
The VIBROT inputs to compute the vibrational-rotational analysis and spectroscopic constants of the state should be:
&VIBROT &END
RoVibrational spectrum
Title
Vib-Rot spectrum for C2. 1Sigmag+
Atoms
0 C 0 C
Grid
400
Range
2.0 10.0
Vibrations
3
Rotations
0 4
Orbital
0
Potential
2.2 -75.42310136
...
End of input
Under the keyword POTEntial the bond distance and
potential energy (both in au) of the corresponding state
must be included. In this case we are going to compute three
vibrational quanta and four rotational quantum numbers.
For the 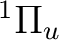 state, the keyword ORBItal must be
set to one, corresponding to the orbital angular momentum
of the computed state. VIBROT fits the potential curve to
an analytical curve using splines. The ro-vibrational
Schrödinger equation is then solved numerically (using
Numerov's method) for one vibrational state at a time and
for the specified number of rotational quantum numbers.
File VIBWVS will contain the corresponding wave
function for further use.
state, the keyword ORBItal must be
set to one, corresponding to the orbital angular momentum
of the computed state. VIBROT fits the potential curve to
an analytical curve using splines. The ro-vibrational
Schrödinger equation is then solved numerically (using
Numerov's method) for one vibrational state at a time and
for the specified number of rotational quantum numbers.
File VIBWVS will contain the corresponding wave
function for further use.
Just to give some of the results obtained, the spectroscopic
constants for the 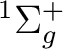 state were:
state were:
Re(a) 1.4461
De(ev) 3.1088
D0(ev) 3.0305
we(cm-1) .126981E+04
wexe(cm-1) -.130944E+02
weye(cm-1) -.105159E+01
Be(cm-1) .134383E+01
Alphae(cm-1) .172923E-01
Gammae(cm-1) .102756E-02
Dele(cm-1) .583528E-05
Betae(cm-1) .474317E-06
and for the 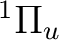 state:
state:
Re(a) 1.3683
De(ev) 2.6829
D0(ev) 2.5980
we(cm-1) .137586E+04
wexe(cm-1) -.144287E+02
weye(cm-1) .292996E+01
Be(cm-1) .149777E+01
Alphae(cm-1) .328764E-01
Gammae(cm-1) .186996E-02
Dele(cm-1) .687090E-05
Betae(cm-1) -.259311E-06
To compute vibrationally averaged TDMs the VIBROT input must be:
&VIBROT &END
Transition moments
Observable
Transition dipole moment
2.2 0.412805
...
End of input
Keyword OBSErvable indicates the start of input
for radial functions of observables other than the energy.
In the present case the vibrational-rotational matrix elements
of the transition dipole moment function will be generated.
The values of the bond distance and the TDM at each distance
must be then included in the input. VIBROT also requires
the VIBWVS1 and VIBWVS2 files
containing the vibrational wave functions of the involved electronic states.
The results obtained contain matrix elements, transition
moments over vibrational wave functions, and the lifetimes of the
transition among all the computed vibrational-rotational states.
The radiative lifetime of a vibrational level depends on the
sum of the transition probabilities to all lower vibrational
levels in all lower electronic states. If rotational effects are
neglected, the lifetime (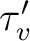 ) can be written as
) can be written as
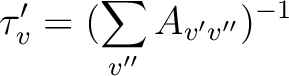 |
(10.1) |
where v' and v'' are the vibrational levels of the lower and upper electronic state and Av'v'' is the Einstein A coefficient (ns-1) computed as
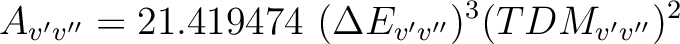 |
(10.2) |
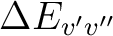 is the energy difference (au) and TDMv'v''
the transition dipole moment (au) of the transition.
is the energy difference (au) and TDMv'v''
the transition dipole moment (au) of the transition.
For instance, for rotational states zero of the 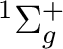 state
and one of the
state
and one of the 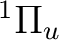 state:
state:
Rotational quantum number for state 1: 0, for state 2: 1
--------------------------------------------------------------------------------
~
Overlap matrix for vibrational wave functions for state number 1
1 1 .307535 2 1 .000000 2 2 .425936 3 1 .000000 3 2 .000000 3 3 .485199
~
Overlap matrix for vibrational wave functions for state number 2
1 1 .279631 2 1 .000000 2 2 .377566 3 1 .000000 3 2 .000000 3 3 .429572
~
Overlap matrix for state 1 and state 2 functions
-.731192 -.617781 -.280533
.547717 -.304345 -.650599
-.342048 .502089 -.048727
~
Transition moments over vibrational wave functions (atomic units)
-.286286 -.236123 -.085294
.218633 -.096088 -.240856
-.125949 .183429 .005284
~
Energy differences for vibrational wave functions(atomic units)
1 1 .015897 2 1 .010246 2 2 .016427 3 1 .004758 3 2 .010939 3 3 .017108
~
Contributions to inverse lifetimes (ns-1)
No degeneracy factor is included in these values.
1 1 .000007 2 1 .000001 2 2 .000001 3 1 .000000 3 2 .000001 3 3 .000000
~
Lifetimes (in nano seconds)
v tau
1 122090.44
2 68160.26
3 56017.08
Probably the most important caution when using the VIBROT program in diatomic molecules is that the number of vibrational states to compute and the accuracy obtained depends strongly on the computed surface. In the present case we compute all the curves to the dissociation limit. In other cases, the program will complain if we try to compute states which lie at energies above those obtained in the calculation of the curve.
10.1.3 A transition metal dimer: Ni2
This section is a brief comment on a complex situation in a diatomic molecule such as Ni2. Our purpose is to compute the ground state of this molecule. An explanation of how to calculate it accurately can be found in ref. [241]. However we will concentrate on computing the electronic states at the CASSCF level.
The nickel atom has two close low-lying configurations 3d84s2 and
3d94s1. The combination of two neutral Ni atoms leads to a
Ni2 dimer whose ground state has been somewhat controversial.
For our purposes we commence with the assumption that it is
one of the states derived
from 3d94s1 Ni atoms, with a single bond between the 4s orbitals,
little 3d involvement, and the holes localized in the 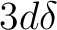 orbitals.
Therefore, we compute the states resulting from two
holes on
orbitals.
Therefore, we compute the states resulting from two
holes on  orbitals:
orbitals:  states.
states.
We shall not go through the procedure leading to the different electronic
states that can arise from these electronic configurations, but refer to
the Herzberg book on diatomic molecules [243] for details. In
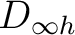 we have three possible configurations with two holes, since the
we have three possible configurations with two holes, since the
 orbitals can be either gerade (g) or ungerade (u):
(
orbitals can be either gerade (g) or ungerade (u):
( )-2, (
)-2, ( )-1(
)-1( )-1, or (
)-1, or ( )-2.
The latter situation corresponds to nonequivalent electrons while the other
two to equivalent electrons.
Carrying through the analysis we obtain the following electronic states:
)-2.
The latter situation corresponds to nonequivalent electrons while the other
two to equivalent electrons.
Carrying through the analysis we obtain the following electronic states:
( )-2 :
)-2 : 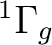 ,
, 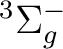 ,
, 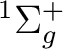
( )-2 :
)-2 : 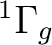 ,
, 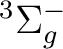 ,
, 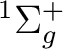
( )-1(
)-1( )-1:
)-1: 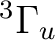 ,
, 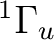 ,
, 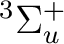 ,
,
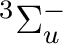 ,
, 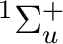 ,
, 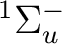
In all there are thus 12 different electronic states.
Next, we need to classify these electronic states in the lower symmetry
D2h, in which MOLCAS works. This is done in Table ![[*]](crossref.png) , which
relates the symmetry in
, which
relates the symmetry in 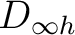 to that of D2h. Since we have only
to that of D2h. Since we have only
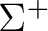 ,
, 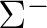 , and
, and 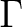 states here, the D2h symmetries
will be only Ag, Au, B1g, and B1u. The table above can
now be rewritten in D2h:
states here, the D2h symmetries
will be only Ag, Au, B1g, and B1u. The table above can
now be rewritten in D2h:
( )-2 : (
)-2 : (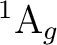 +
+
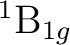 ),
),
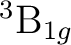 ,
, 
( )-2 : (
)-2 : ( +
+
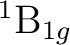 ),
),
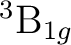 ,
, 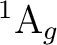
( )-1(
)-1( )-1: (
)-1: (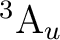 +
+
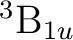 ), (
), (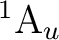 +
+
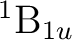 ),
),
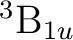 ,
, 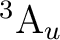 ,
,
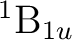 ,
, 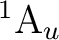
or, if we rearrange the table after the D2h symmetries:
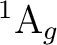 :
: 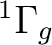 (
( )-2,
)-2, 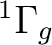 (
( )-2,
)-2,
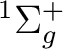 (
( )-2,
)-2, 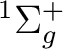 (
( )-2
)-2
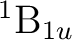 :
: 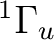 (
( )-1(
)-1( )-1,
)-1,
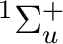 (
( )-1(
)-1( )-1
)-1
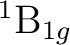 :
: 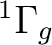 (
( )-2,
)-2, 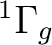 (
( )-2
)-2
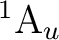 :
: 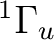 (
( )-1(
)-1( )-1,
)-1,
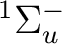 (
( )-1(
)-1( )-1
)-1
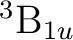 :
:  (
( )-1(
)-1( )-1,
)-1,
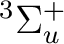 (
( )-1(
)-1( )-1
)-1
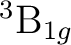 :
: 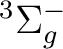 (
( )-2,
)-2, 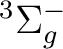 (
( )-2
)-2
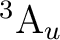 :
: 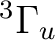 (
( )-1(
)-1( )-1,
)-1,
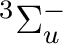 (
( )-1(
)-1( )-1
)-1
It is not necessary to compute all the states because some of
them (the  states) have degenerate components. It is both
possible to make single state calculations looking for the lowest
energy state of each symmetry or state-average calculations in each of
the symmetries. The identification of the
states) have degenerate components. It is both
possible to make single state calculations looking for the lowest
energy state of each symmetry or state-average calculations in each of
the symmetries. The identification of the 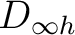 states can be
somewhat difficult. For instance, once we have computed one
states can be
somewhat difficult. For instance, once we have computed one
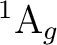 state it can be a
state it can be a 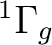 or a
or a 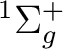 state.
In this case the simplest solution is to compare the obtained
energy to that of the
state.
In this case the simplest solution is to compare the obtained
energy to that of the 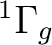 degenerate component in
B1g symmetry, which must be equal to the energy of the
degenerate component in
B1g symmetry, which must be equal to the energy of the
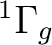 state computed in Ag symmetry. Other situations
can be more complicated and require a detailed analysis of the
wave function.
state computed in Ag symmetry. Other situations
can be more complicated and require a detailed analysis of the
wave function.
It is important to have clean d-orbitals and the SUPSym
keyword may be needed to separate  and
and  (and
(and 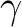 if g-type functions are used in the basis set)
orbitals in symmetry 1 (Ag). The AVERage keyword
is not needed here because the
if g-type functions are used in the basis set)
orbitals in symmetry 1 (Ag). The AVERage keyword
is not needed here because the  and
and  orbitals have
the same occupation for
orbitals have
the same occupation for 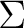 and
and 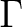 states.
states.
Finally, when states of different multiplicities are close in
energy, the spin-orbit coupling which mix the different states
should be included. The CASPT2 study of the Ni2 molecule
in reference [241], after considering all the mentioned
effects determined that the ground
state of the molecule is a 0g+ state, a mixture of the
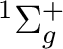 and
and 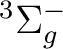 electronic states.
For a review of the spin-orbit coupling and other important
coupling effects see reference [246].
electronic states.
For a review of the spin-orbit coupling and other important
coupling effects see reference [246].
10.1.4 High symmetry systems in MOLCAS
There are a large number of symmetry point groups in which MOLCAS cannot directly work. Although unusual in organic chemistry, some of them can be easily found in inorganic compounds. Systems belonging for instance to three-fold groups such as C3v, D3h, or D6h, or to groups such Oh or D4h must be computed using lower symmetry point groups. The consequence is, as in linear molecules, that orbitals and states belonging to different representations in the actual groups, belong to the same representation in the lower symmetry case, and vice versa. In the RASSCF program it is possible to prevent the orbital and configurational mixing caused by the first situation. The CLEAnup and SUPSymmetry keywords can be used in a careful, and somewhat tedious, way. The right symmetry behaviour of the RASSCF wave function is then assured. It is sometimes not a trivial task to identify the symmetry of the orbitals in the higher symmetry representation and which coefficients must vanish. In many situations the ground state wave function keeps the right symmetry (at least within the printing accuracy) and helps to identify the orbitals and coefficients. It is more frequent that the mixing happens for excited states.
The reverse situation, that is, that orbitals (normally degenerated) which belong to the same symmetry representation in the higher symmetry groups belong to different representations in the lower symmetry groups cannot be solved by the present implementation of the RASSCF program. The AVERage keyword, which performs this task in the linear molecules, is not prepared to do the same in non-linear systems. Provided that the symmetry problems mentioned in the previous paragraph are treated in the proper way and the trial orbitals have the right symmetry, the RASSCF code behaves properly.
There is a important final precaution concerning the high symmetry systems:
the geometry of the molecule must be of the right symmetry. Any deviation
will cause severe mixings. Figure ![[*]](crossref.png) contains the
SEWARD input for the magnesium porphirin molecule. This is
a D4h system which must be computed D2h in MOLCAS.
contains the
SEWARD input for the magnesium porphirin molecule. This is
a D4h system which must be computed D2h in MOLCAS.
For instance, the x and y coordinates of atoms C1 and C5 are interchanged with equal values in D4h symmetry. Both atoms must appear in the SEWARD input because they are not independent by symmetry in the D2h symmetry in which MOLCAS is going to work. Any deviation of the values, for instance to put the y coordinate to 0.681879 Å in C1 and the x to 0.681816 Å in C5 and similar deviations for the other coordinates, will lead to severe symmetry mixtures. This must be taken into account when geometry data are obtained from other program outputs or data bases.
 |
&SEWARD &END
Title
Mg-Porphyrine D4h computed D2h
Symmetry
X Y Z
Basis set
C.ANO-S...3s2p1d.
C1 4.254984 .681879 .000000 Angstrom
C2 2.873412 1.101185 0.000000 Angstrom
C3 2.426979 2.426979 0.000000 Angstrom
C4 1.101185 2.873412 0.000000 Angstrom
C5 .681879 4.254984 0.000000 Angstrom
End of basis
Basis set
N.ANO-S...3s2p1d.
N1 2.061400 .000000 0.000000 Angstrom
N2 .000000 2.061400 0.000000 Angstrom
End of basis
Basis set
H.ANO-S...2s0p.
H1 5.109145 1.348335 0.000000 Angstrom
H3 3.195605 3.195605 0.000000 Angstrom
H5 1.348335 5.109145 0.000000 Angstrom
End of basis
Basis set
Mg.ANO-S...4s3p1d.
Mg .000000 .000000 0.000000 Angstrom
End of basis
End of Input
The situation can be more complex for some three-fold point groups such as D3h or C3v. In these cases it is not possible to input in the exact cartesian geometry, which depends on trigonometric relations and relies on the numerical precision of the coordinates entry. It is necessary then to use in the SEWARD input as much precision as possible and check on the distance matrix of the SEWARD output if the symmetry of the system has been kept at least within the output printing criteria.
Next: 10.2 Geometry optimizations and Hessians. Up: 10. Examples Previous: 10. Examples


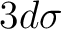 correlation comprises the singly occupied 3dxy orbital and three
correlation comprises the singly occupied 3dxy orbital and three  and
and 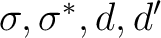 ) that is the most consistent choice of active orbitals as
evidenced in the calculation of other metal hydrides such as CuH [
) that is the most consistent choice of active orbitals as
evidenced in the calculation of other metal hydrides such as CuH [