





















MOLCAS manual: Next: 9. GUI Up: 8. Programs Previous: 8.50 wfa
The basis sets library contains both all-electron and effective core
potentials. They will be briefly described below and we
refer to the publications for more details. The user can also add new
basis sets to the basis directory and the structure of the file will therefore
be described below.
|
| Li–B: | 1s |
| C–Ne: | No core correlation |
| Na: | 2s,2p |
| Mg–Al: | 2p |
| Si–Ar: | No core correlation |
| K: | 3s,3p |
| Ca–Zn: | 3p |
| Ga–Ge: | 3d |
| As–Kr: | No core correlation |
| Rb–Sr: | 4p |
| In–Xe: | 4d |
| Cs–Ba: | 5p |
| La–Lu: | 5s,5p |
| Hf–Re: | 4f,5s,5p |
| Os–Hg: | 5s,5p |
| Tl–Rn: | 5d |
| Fr–Ra: | 6p |
| Ac-Cm: | 6s,6p |
Basis set label in input:
The general label is given as for the other ANO basis sets:
Atom.ano-rcc...contracted set. (Note the last dot!).
A short hand notation is also possible:
Atom.ANO-RCC-label, where label is one of MB,VDZ,VDZP,VTZP, or VQZP.
A translation between the two possibilities can be found in file:
$MOLCAS/basis_library/basis.tbl
8.51.0.2.4 Polarized basis sets
The so-called polarized basis sets are purpose oriented, relatively small GTO/CGTO sets devised for the purpose of accurate calculations of dipole electric properties of polyatomic molecules [187,188,189,190,191]. For each row of the periodic table the performance of the basis sets has been carefully examined in calculations of dipole moments and dipole polarizabilities of simple hydrides at both the SCF and correlated levels of approximation [187,188,189,190,191]. The corresponding results match within a few percent the best available experimental data. Also the calculated molecular quadrupole moments turn out to be fairly close to those computed with much larger basis sets. According to the present documentation the polarized basis GTO/CGTO sets can be used for safe accurate predictions of molecular dipole moments, dipole polarizabilities, and also molecular quadrupole moments by using high-level correlated computational methods. The use of the polarized basis sets has also been investigated in calculations of weak intermolecular interactions. The interaction energies, corrected for the basis set superposition effect (BSSE), which is rather large for these basis sets, turn out to be close to the best available data. In calculations for molecules involving the 4th row atoms, the property data need to be corrected for the relativistic contribution. The corresponding finite perturbation facility is available [192,193].
It is recommended to use these basis sets with the contraction given in the library. It is of course possible to truncate them further, for example by deleting some polarization functions, but this will lead to a deterioration of the computed properties.
8.51.0.3 Structure of the all electron basis set library
The start of a given basis set in the library is given by the line
| /label |
where ``label'' is the basis set label, as defined below in the input description to SEWARD. Then follows two lines with the appropriate literature reference for that basis set. These cards are read by SEWARD and must thus be included in the library, and may not be blank. Next is a set of comment lines, which begin with an asterisk in column 1, giving some details of the basis sets. A number of lines follow, which specifies the basis set:
- Charge of the atom and the highest angular momentum. For each angular momentum (l) then follows.
- Number of primitives and contracted functions for angular momentum l (must be identical to those given in the basis set label) .
- Exponents of the primitive functions .
- The contraction matrix (with one CGTO per column). Note that all basis sets are given in the generally contracted format, even if they happen to be segmented. Note that the number of CGTOs must correspond to the data given in the label .
The following is an example of an entry in a basis set library.
* This is the Huzinaga 5s,2p set contracted to 3s,2p -- Comment
* according to the Dunning paper. -- Comment
/H.TZ2P.Dunning.5s2p.3s2p. -- Label
Exponents : S. Huzinaga, J. Chem. Phys., 42, 1293(1965). -- First ref line
Coefficients: T. H. Dunning, J. Chem. Phys., 55, 716(1971). -- Second ref line
1.0 1 -- Charge, sp
5 3 -- 5s->3s
52.56 7.903 1.792 0.502 0.158 -- s-exponents
0.025374 0.0 0.0 -- contr. matrix
0.189684 0.0 0.0 -- contr. matrix
0.852933 0.0 0.0 -- contr. matrix
0.0 1.0 0.0 -- contr. matrix
0.0 0.0 1.0 -- contr. matrix
2 2 -- 2p->2p
1.5 0.5 -- p-exponents
1.0 0.0 -- contr. matrix
0.0 1.0 -- contr. matrix
8.51.0.4 The ECP Library
MOLCAS is able to perform effective core potential (ECP) calculations and embedded cluster calculations. In ECP calculations, only the valence electrons of a molecule are explicitly handled in a quantum mechanical calculation, at a time that the core electrons are kept frozen and are represented by ECP's. (An example of this is a calculation on HAt in which only the 5d, 6s and 6p electrons of Astatine and the one of Hydrogen are explicitly considered.) Similarly, in embedded cluster calculations, only the electrons assigned to a piece of the whole system (the cluster) are explicitly handled in the quantum mechanical calculation, under the assumption that they are the only ones relevant for some local properties under study; the rest of the whole system (the environment) is kept frozen and represented by embedding potentials which act onto the cluster. (As an example, calculations on a TlF1211- cluster embedded in a frozen lattice of KMgF3 can be sufficient to calculate spectroscopical properties of Tl+-doped KMgF3 which are due to the Tl+ impurity.)
In order to be able to perform ECP calculations in molecules, as well as embedded cluster calculations in ionic solids, with the Ab Initio Model Potential method (AIMP) [194,195,196,197,198,199] MOLCAS is provided with the library ECP which includes nonrelativistic and relativistic core ab initio model potentials and embedding ab initio model potentials representing both complete-cations and complete-anions in ionic lattices [195,200].
Before we continue we should comment a little bit on the terminology used here. Strictly speaking, ECP methods are all that use the frozen-core approximation. Among them, we can distinguish two families: the `pseudopotential' methods and the `model potential' methods. The pseudopotential methods are ultimately based on the Phillips-Kleinman equation [201] and handle valence nodeless pseudo orbitals. The model potential methods are based on the Huzinaga equation [202,203] and handle node-showing valence orbitals; the AIMP method belongs to this family. Here, when we use the general term ECP we will be referring to the more particular of AIMP. According to its characteristics, the AIMP method can be also applied to represent frozen-ions in ionic lattices in embedded cluster calculations; in this case, we will not be very strict in the nomenclature and we will also call ECP's to the frozen-ion (embedding) ab initio model potentials.
The effective potentials in the libraries include the effects of the atomic core wave functions (embedding ion wave functions) through the following operators:
- a local representation of the core (ion) Coulomb operator,
- a non-local spectral representation of the core (ion) exchange operator,
- a core (ion) projection operator,
- a spectral representation of the relativistic mass-velocity and Darwin operators corresponding to the valence orbitals, if the Cowan-Griffin-based scalar relativistic CG-AIMP method [196] is used.
- a spectral representation of the relativistic no-pair Douglas-Kroll operators, if the scalar relativistic no-pair Douglas-Kroll NP-AIMP method [197,198,199] is used.
Given the quality and non-parametric nature of the operators listed above, the flexibility of the basis sets to be used with the AIMP's is crucial, as in any ab initio method.
The valence basis sets included in the libraries have been obtained by energy minimization in atomic valence-electron calculations, following standard optimization procedures. All the experience gathered in the design of molecular basis sets starting from all-electron atomic basis sets, and in particular from segmented minimal ones, is directly applicable to the AIMP valence basis sets included in the libraries. They are, for non-relativistic and relativistic Cowan-Griffin AIMPs, minimal basis sets with added functions, such as polarization and diffuse functions; in consequence, the minimal sets should be split in molecular calculations in order to get reasonable sets (a splitting pattern is recommended in the library for every set); the splitting can be done by means of `the basis set label'. For the relativistic no-pair Douglas-Kroll AIMPs contracted valence basis sets are given directly in a form which is recommended in molecular calculations, i.e. they are of triple zeta quality in the outer shells and contain polarization functions. In both cases these valence basis sets contain very inner primitive GTF's: They are necessary since, typical to a model potential method, the valence orbitals will show correct nodal structure. Finally, it must be noted that the core AIMP's can be safely mixed together with all-electron basis sets.
In AIMP embedded cluster calculations, the cluster basis set, which must be decided upon by the user, should be designed following high quality standard procedures. Very rigid cluster basis sets should not be used. In particular, the presence of the necessary embedding projection operators, which prevent the cluster densities from collapsing onto the crystal lattice, demands flexible cluster bases, including, eventually, components outside the cluster volume.[204] The use of flexible cluster basis sets is then a necessary requirement to avoid artificial frontier effects, not ascribable to the AIMP embedding potentials. This requirement is unavoidable, anyway, if good correlated wave functions are to be calculated for the cluster. Finally, one must remember that the AIMP method does exclude any correlation between the cluster electronic group and the embedding crystal components; in other words, only intra-cluster correlation effects can be accounted for in AIMP embedded cluster calculations. Therefore the cluster-environment partition and the choice of the cluster wave function must be done accordingly. In particular, the use of one-atom clusters is not recommended.
Core- and embedding- AIMP's can be combined in a natural way in valence-electron, embedded cluster calculations. They can be used with any of the different types of wave functions that can be calculated with MOLCAS.
8.51.0.4.1 Core AIMP's
The list of core potentials and valence basis sets available in the ECP library follows. Although AIMP's exist in the literature for different core sizes, this library includes only those recommended by the authors after numerical experimentation. Relativistic CG-AIMP's and NP-AIMP's, respectively, and nonrelativistic NR-AIMP's are included. Each entry of the CG-AIMP's and the NR-AIMP's in the list is accompanied with a recommended contraction pattern (to be used in the fifth field). The NP-AIMP basis sets are given explicitly in the recommended contraction pattern. For the third-row transition metals two NP-AIMP basis sets are provided which differ in the number of primitive and contracted f GTFs. For further details, please refer to the literature.[199] For more information about a particular entry consult the ECP library.
The ECP libraries have also been extended to include the so-called nodeless ECPs or pseudo potentials based on the Phillips-Kleinman equation [201]. These are included both as explicit and implicit operators. Following the work by M. Pelissier and co-workers [205] the operators of nodeless ECPs can implicitly be fully expressed via spectral representation of operators. The explicit libraries are the ECP.STOLL and ECP.HAY-WADT files, all other files are for the implicitly expressed operator. In the list of nodeless ECPs the Hay and Wadt's family of ECPs (LANL2DZ ECPs) [206,207,208] has been included in addition to the popular set of the so-called Stoll and Dolg ECPs [209,210,211,212,213,214,215,216,217,218,219,220,221,222,223,224,225,226,227,228,229,230,231,232,233]. Both of them in either the explicit form labeled as HAY-WADT and STOLL, or in the implicit form labeled as HW and DOLG. The latter include the recently developed ANO-basis sets for actinides [233].
8.51.0.5 Structure of the ECP libraries
The start of a given basis set and AIMP is identified by the line

where ``label" is defined below,
in the input description to seward.
Then, comment lines, effective charge, and basis set follow,
with the same structure that the all-electron Basis Set Library
(see items 1. to 4. in Sec. ![[*]](crossref.png) .)
Next, the AIMP/ECP/PP is specified as follows:
.)
Next, the AIMP/ECP/PP is specified as follows:
- The pseudo potential approach [234,235,236],
see eqs. (3) and (4) in Ref. [237],
with the following lines:
- The keyword PP
On the same line follows the atomic symbol of the element, the number of core electrons (Nc) and
L, where L-1 is the largest angular momentum orbital belonging to the core. This line
is followed by L+1 identical sections. The first of these sections is the so-called L potential
and the subsequent sections corresponds to the S-L, P-L, D-L, etc. potentials.
Each sections start with a line specifying the number of Gaussian terms in the potential.
This line is then followed by a single line for each Gaussian specifying
the powers (nkl), the Gaussian exponent (
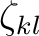 ), and the associated coefficient
(dkl).
), and the associated coefficient
(dkl).
Note that the pseudo potential input is mutually exclusive to the M1, M2, COREREP, and PROJOP keywords!
- The keyword PP
On the same line follows the atomic symbol of the element, the number of core electrons (Nc) and
L, where L-1 is the largest angular momentum orbital belonging to the core. This line
is followed by L+1 identical sections. The first of these sections is the so-called L potential
and the subsequent sections corresponds to the S-L, P-L, D-L, etc. potentials.
Each sections start with a line specifying the number of Gaussian terms in the potential.
This line is then followed by a single line for each Gaussian specifying
the powers (nkl), the Gaussian exponent (
- The Coulomb local model potential, eq.(6) in Ref. [194]
with the following lines:
- The keyword M1, which identifies the terms with nk=0.
- The number of terms.
If greater than 0, lines
![[*]](crossref.png) and
and ![[*]](crossref.png) are read.
are read.
- The exponents
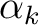 .
.
- The coefficients Ak (divided by the negative of the effective charge).
- The keyword M2, which identifies the terms with nk=1.
- The number of terms.
If greater than 0, lines
![[*]](crossref.png) and
and ![[*]](crossref.png) are read.
are read.
- The exponents
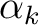 .
.
- The coefficients Ak (divided by the negative of the effective charge).
- A line with the keyword COREREP followed by another one with a real constant. This is not used now but it is reserved for future use.
- The projection operator, eq.(3) in Ref. [194]
with the following lines:
- The keyword PROJOP.
- The maximum angular momentum (l)
of the frozen core (embedding) orbitals.
Lines
![[*]](crossref.png) to
to ![[*]](crossref.png) are repeated for
each angular momentum l.
are repeated for
each angular momentum l.
- The number of primitives and the number of orbitals (more properly, degenerate sets of orbitals or l-shells) for angular momentum l. As an option, these two integers can be followed by the occupation numbers of the l-shells; default values are 2 for l=0, 6 for l=1, etc.
- The projection constants,
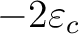 .
.
- The exponents of the primitive functions.
- The coefficients of the orbitals, one per column, using general contraction format.
- The spectral representation operator,
eq.(7) in Ref. [194] for NR-AIMP,
eq.(3) in Ref. [196] for relativistic CG-AIMP,
and eqs.(1) and (7) in Ref. [199] for relativistic NP-AIMP,
with the following lines:
- The keyword Spectral Representation Operator.
- One of the keywords
Valence, Core, or External.
Valence indicates that the set of primitive functions specified
in the basis set data will be used for the spectral representation
operator;
this is the standard for ab initio core model potentials.
Core means that the set of primitives specified
in the PROJOP section will be used instead;
this is the standard for complete-ion ab initio embedding model
potentials.
External means that a set of primitives specific for the
spectral representation operator will be provided in the next lines.
In this case the format is
one line in which an integer number specifies the highest angular momentum
of the external basis sets; then, for each angular momentum the input is
formated as for lines
![[*]](crossref.png) ,
, ![[*]](crossref.png) , and
, and ![[*]](crossref.png) in Sec.
in Sec. ![[*]](crossref.png) .
.
- The keyword Exchange.
- For relativistic AIMPs one of the keywords NoPair or 1stOrder Relativistic Correction. NoPair indicates that scalar relativistic no-pair Douglas-Kroll AIMP integrals are to be calculated. 1stOrder Relativistic Correction means that Cowan-Griffin-based scalar relativistic AIMP, CG-AIMP's, are used. In the latter case, in the next line a keyword follows which, in the library QRPLIB, identifies the starting of the numerical mass-velocity plus Darwin potentials (eq.(2) in Ref. [196]). (In QRPLIB a line with ``keyword mv&dw potentials start" must exist, followed by the number of points in the radial logarithmic grid, the values of the radial coordinate r, and, for each valence orbital, its label (2S, 4P, etc), and the values of the mass-velocity plus Darwin potentials at the corresponding values of r; these data must end up with a line ``keyword mv&dw potentials end".)
- The keyword End of Spectral Representation Operator.
Below is an example of an entry in the ECP library for an AIMP.
/S.ECP.Barandiaran.7s6p1d.1s1p1d.6e-CG-AIMP. -- label (note that type is ECP)
Z.Barandiaran and L.Seijo, Can.J.Chem. 70(1992)409. -- 1st ref. line
core[Ne] val[3s,3p] (61/411/1*)=2s3p1d recommended -- 2nd ref. line
*SQR-SP(7/6/1) (61/411/1) -- comment line
6.000000 2 -- eff. charge & highest ang.mom.
-- blank line
7 1 -- 7s -> 1s
1421.989530 -- s-exponent
211.0266560 -- s-exponent
46.72165060 -- s-exponent
4.310564040 -- s-exponent
1.966475840 -- s-exponent
.4015383790 -- s-exponent
.1453058790 -- s-exponent
.004499703540 -- contr. coeff.
.030157124800 -- contr. coeff.
.089332590700 -- contr. coeff.
-.288438151000 -- contr. coeff.
-.279252515000 -- contr. coeff.
.700286615000 -- contr. coeff.
.482409523000 -- contr. coeff.
6 1 -- 6p -> 1p
78.08932440 -- p-exponent
17.68304310 -- p-exponent
4.966340810 -- p-exponent
.5611646780 -- p-exponent
.2130782690 -- p-exponent
.8172415400E-01 -- p-exponent
-.015853278200 -- contr. coeff.
-.084808963800 -- contr. coeff.
-.172934245000 -- contr. coeff.
.420961662000 -- contr. coeff.
.506647309000 -- contr. coeff.
.200082121000 -- contr. coeff.
1 1 -- 1d -> 1d
.4210000000 -- d-exponent
1.000000000000 -- contr. coeff.
* -- comment line
* Core AIMP: SQR-2P -- comment line
* -- comment line
* Local Potential Parameters : (ECP convention) -- comment line
* A(AIMP)=-Zeff*A(ECP) -- comment line
M1 -- M1 operator
9 -- number of M1 terms
237485.0100 -- M1 exponent
24909.63500 -- M1 exponent
4519.833100 -- M1 exponent
1082.854700 -- M1 exponent
310.5610000 -- M1 exponent
96.91851000 -- M1 exponent
26.63059000 -- M1 exponent
9.762505000 -- M1 exponent
4.014487500 -- M1 exponent
-- blank line
.019335998333 -- M1 coeff.
.031229360000 -- M1 coeff.
.061638463333 -- M1 coeff.
.114969451667 -- M1 coeff.
.190198283333 -- M1 coeff.
.211928633333 -- M1 coeff.
.336340950000 -- M1 coeff.
.538432350000 -- M1 coeff.
.162593178333 -- M1 coeff.
M2 -- M2 operator
0 -- number of M2 terms
COREREP -- CoreRep operator
1.0 -- CoreRep constant
PROJOP -- Projection operator
1 -- highest ang. mom.
8 2 -- 8s -> 2s
184.666320 18.1126960 -- 1s,2s proj. op. constants
3459.000000 -- s-exponent
620.3000000 -- s-exponent
171.4000000 -- s-exponent
58.53000000 -- s-exponent
22.44000000 -- s-exponent
6.553000000 -- s-exponent
2.777000000 -- s-exponent
1.155000000 -- s-exponent
.018538249000 .005054826900 -- contr. coeffs.
.094569248000 .028197248000 -- contr. coeffs.
.283859290000 .088959130000 -- contr. coeffs.
.454711270000 .199724180000 -- contr. coeffs.
.279041370000 .158375340000 -- contr. coeffs.
.025985763000 -.381198090000 -- contr. coeffs.
-.005481472900 -.621887210000 -- contr. coeffs.
.001288714400 -.151789890000 -- contr. coeffs.
7 1 -- 7p -> 1p
13.3703160 -- 2p proj. op. constant
274.0000000 -- p-exponent
70.57000000 -- p-exponent
24.74000000 -- p-exponent
9.995000000 -- p-exponent
4.330000000 -- p-exponent
1.946000000 -- p-exponent
.8179000000 -- p-exponent
.008300916100 -- cont. coeff.
.048924254000 -- cont. coeff.
.162411660000 -- cont. coeff.
.327163550000 -- cont. coeff.
.398615170000 -- cont. coeff.
.232548200000 -- cont. coeff.
.034091088000 -- cont. coeff.
* -- comment line
Spectral Representation Operator -- SR operator
Valence primitive basis -- SR basis specification
Exchange -- Exchange operator
1stOrder Relativistic Correction -- mass-vel + Darwin oper.
SQR-2P -- label in QRPLIB
End of Spectral Representation Operator -- end of SR operator
Below is an example of an entry in the ECP library for a pseudo potential.
/Hg.ECP.Dolg.4s4p2d.2s2p1d.2e-MWB -- label (note the type ECP)
W. Kuechle, M. Dolg, H. Stoll, H. Preuss, Mol. Phys.-- ref. line 1
74, 1245 (1991); J. Chem. Phys. 94, 3011 (1991). -- ref. line 2
2.00000 2 -- eff. charge & highest ang.mom.
*s functions -- comment line
4 2 -- 4s -> 2s
0.13548420E+01 -- s-exponent
0.82889200E+00 -- s-exponent
0.13393200E+00 -- s-exponent
0.51017000E-01 -- s-exponent
0.23649400E+00 0.00000000E+00 -- contr. coeff.
-0.59962800E+00 0.00000000E+00 -- contr. coeff.
0.84630500E+00 0.00000000E+00 -- contr. coeff.
0.00000000E+00 0.10000000E+01 -- contr. coeff.
*p functions -- comment line
4 2 -- 4p -> 2p
0.10001460E+01 -- p-exponent
0.86645300E+00 -- p-exponent
0.11820600E+00 -- p-exponent
0.35155000E-01 -- p-exponent
0.14495400E+00 0.00000000E+00 -- contr. coeff.
-0.20497100E+00 0.00000000E+00 -- contr. coeff.
0.49030100E+00 0.00000000E+00 -- contr. coeff.
0.00000000E+00 0.10000000E+01 -- contr. coeff.
*d functions -- comment line
1 1 -- 1d -> 1d
0.19000000E+00 -- d-exponent
0.10000000E+01 -- contr. coeff.
* -- comment line
PP,Hg,78,5; -- PP operator, label, # of core elec., L
1; ! H POTENTIAL -- # number of exponents in the H potential
2, 1.00000000,.000000000; -- power, exponent and coeff.
3; ! S-H POTENTIAL -- # number of exponents in the S-H potential
2,0.227210000,-.69617800; -- power, exponent and coeff.
2, 1.65753000,27.7581050; -- power, exponent and coeff.
2, 10.0002480,48.7804750; -- power, exponent and coeff.
2; ! P-H POTENTIAL -- # number of exponents in the P-H potential
2,0.398377000,-2.7358110; -- power, exponent and coeff.
2,0.647307000,8.57563700; -- power, exponent and coeff.
2; ! D-H POTENTIAL -- # number of exponents in the D-H potential
2,0.217999000,-.01311800; -- power, exponent and coeff.
2,0.386058000,2.79286200; -- power, exponent and coeff.
1; ! F-H POTENTIAL -- # number of exponents in the F-H potential
2,0.500000000,-2.6351640; -- power, exponent and coeff.
1; ! G-H POTENTIAL -- # number of exponents in the G-H potential
2,0.800756000,-13.393716; -- power, exponent and coeff.
* -- comment line
Spectral Representation Operator -- SR operator
End of Spectral Representation Operator -- end of SR operator
Next: 9. GUI Up: 8. Programs Previous: 8.50 wfa

