





















MOLCAS manual: Next: 8.50 wfa Up: 8. Programs Previous: 8.48 surfacehop
|
| Keyword | Meaning |
| ROVIbrational spectrum | VIBROT will perform a vib-rot analysis and compute spectroscopic constants. |
| TRANsition moments | VIBROT will compute transition moment integrals using results from two previous calculations of the vib-rot wave functions. In this case the keyword Observable should be included, and it will be interpreted as the transition dipole moment. |
After this first keyword follows a set of keywords, which are used to specify the run. Most of them are optional.
The compulsory keywords are:
| Keyword | Meaning |
| ATOMs | Gives the mass of the two atoms. Write mass number (an integer) and the chemical symbol Xx, in this order, for each of the two atoms in free format. If the mass numbers is zero for any atom, the mass of the most abundant isotope will be used. All isotope masses are stored in the program. You may introduce your own masses by giving a negative integer value to the mass number (one of them or both). The masses (in unified atomic mass units, or Da) are then read on the next (or next two) entry(ies). The isotopes of hydrogen can be given as H, D, or T. |
| POTEntial | Gives the potential as an arbitrary number of lines. Each line contains a bond distance (in au) and an energy value (in au). A plot file of the potential is generated if the keyword Plot is added after the last energy input. One more entry should then follow with three numbers specifying the start and end value for the internuclear distance and the distance between adjacent plot points. This input must only be given together with the keyword RoVibrational spectrum. |
In addition you may want to specify some of the following optional input:
| Keyword | Meaning |
| TITLe | One single title line |
| GRID | The next entries give the number of grid points used in the numerical solution of the radial Schrödinger equation. The default value is 199. The maximum value that can be used is 4999. |
| RANGe | The next entry contains two distances Rmin and Rmax (in au) specifying the range in which the vibrational wave functions will be computed. The default values are 1.0 and 5.0 au. Note that these values most often have to be given as input since they vary considerably from one case to another. If the range specified is too small, the program will give a message informing the user that the vibrational wave function is large outside the integration range. |
| VIBRational | The next entry specifies the number of vibrational quanta for which the wave functions and energies are computed. Default value is 3. |
| ROTAtional | The next entry specifies the range of rotational quantum numbers.
Default values are 0 to 5. If the orbital angular momentum quantum
number (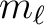 ) is non zero, the lower value will be adjusted to ) is non zero, the lower value will be adjusted to
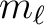 if the start value given in input is smaller than if the start value given in input is smaller than
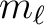 . .
|
| ORBItal | The next entry specifies the value of the orbital angular momentum (0,1,2, etc). Default value is zero. |
| SCALe | This keyword is used to scale the potential, such that the binding energy is 0.1 au. This leads to better precision in the numerical procedure and is strongly advised for weakly bound potentials. |
| NOSPectroscopic | Only the wave function analysis will be carried out but not the calculation of spectroscopic constants. |
| OBSErvable | This keyword indicates the start of input for radial functions of observables other than the energy, for example the dipole moment function. The next line gives a title for this observable. An arbitrary number of input lines follows. Each line contains a distance and the corresponding value for the observable. As for the potential, this input can also end with the keyword Plot, to indicate that a file of the function for later plotting is to be constructed. The next line then contains the minimum and maximum R-values and the distance between adjacent points. When this input is given with the top keyword RoVibrational spectrum the program will compute matrix elements for vibrational wave functions of the current electronic state. Transition moment integrals are instead obtained when the top keyword is Transition moments. In the latter case the calculation becomes rather meaningless if this input is not provided. The program will then only compute the overlap integrals between the vibrational wave functions of the two states. The keyword Observable can be repeated up to ten times in a single run. All observables should be given in atomic units. |
| TEMPerature | The next entry gives the temperature (in K) at which the vibrational averaging of observables will be computed. The default is 300 K. |
| STEP | The next entry gives the starting value for the energy step used in the bracketing of the eigenvalues. The default value is 0.004 au (88 cm-1). This value must be smaller than the zero-point vibrational energy of the molecule. |
| ASYMptotic | The next entries specifies the asymptotic energy difference between two potential curves in a calculation of transition matrix elements. The default value is zero atomic units. |
| ALLRotational | By default, when the Transition moments keyword is given, only the transitions between the lowest rotational level in each vibrational state are computed. The keyword AllRotational specifies that the transitions between all the rotational levels are to be included. Note that this may result in a very large output file. |
| PRWF | Requests the vibrational wave functions to be printed in the output file. |
8.49.3.2 Input example
&VIBROT
RoVibrational spectrum
Title = Vib-Rot spectrum for FeNi
Atoms = 0 Fe 0 Ni
Potential
1.0 -0.516768
1.1 -0.554562
[...]
Plot = 1.0 10.0 0.1
Grid = 150
Range = 1.0 10.0
Vibrations = 10
Rotations = 2 10
Orbital = 2
Observable
Dipole Moment
1.0 0.102354
1.1 0.112898
[...]
Plot = 1.0 10.0 0.1
Comments: The vibrational-rotation spectrum for FeNi will be computed using the potential curve given in input. The 10 lowest vibrational levels will be obtained and for each level the rotational states in the range J=2 to 10. The vib-rot matrix elements of the dipole function will also be computed. A plot file of the potential and the dipole function will be generated. The masses for the most abundant isotopes of Fe and Ni will be selected.
Next: 8.50 wfa Up: 8. Programs Previous: 8.48 surfacehop

